统计 - 正态分布

正态分布是统计学中一个重要的概率分布。

许多现实世界的数据都呈正态分布。

正态分布

正态分布由均值 (\(\mu\)) 和标准差 (\(\sigma\)) 描述。

正态分布由于其形状，通常被称为“钟形曲线”。

• 大多数值都集中在中心 (\(\mu\)) 附近。
• 中位数和均值相等。
• 它只有一个众数。
• 它具有对称性，这意味着它在中心两侧的下降量相同。

正态分布曲线下的面积代表数据的概率。

整个曲线下的面积等于 1，即 100%。

这是正态分布在标准差 (\(\sigma\)) 之间的概率图。

• 大约 68.3% 的数据在平均值（从 μ-1σ 到 μ+1σ）的一个标准差范围内。
• 大约 95.5% 的数据在平均值的两个标准差范围内（从 μ-2σ 到 μ+2σ）。
• 大约 99.7% 的数据在平均值的三个标准差范围内（从 μ-3σ 到 μ+3σ）。

不同的均值和标准差

均值描述了正态分布的中心位置。

这是一张显示三个具有相同标准差但均值不同的正态分布的图。

标准差描述了正态分布的扩散程度。

这是一张显示三个具有相同均值但标准差不同的正态分布的图。

紫色曲线的标准差最大，黑色曲线的标准差最小。

每条曲线下的面积仍然是 1，即 100%。

正态分布数据的真实数据示例

现实世界的数据通常呈正态分布。

这是一个诺贝尔奖获得者获奖时的年龄直方图。

绘制在直方图上方的正态分布是基于真实数据的总体均值 (\(\mu\)) 和标准差 (\(\sigma\))。

我们可以看到直方图接近正态分布。

可能呈正态分布的现实世界变量的示例

• 考试成绩
• 高度
• 出生体重

概率分布

概率分布是计算随机变量结果概率的函数。

随机变量的典型示例是抛硬币和掷骰子。

这是一张图，显示了抛硬币次数不断增加的结果以及预期的结果（正面或反面）。

抛硬币的预期值是抛硬币的概率分布。

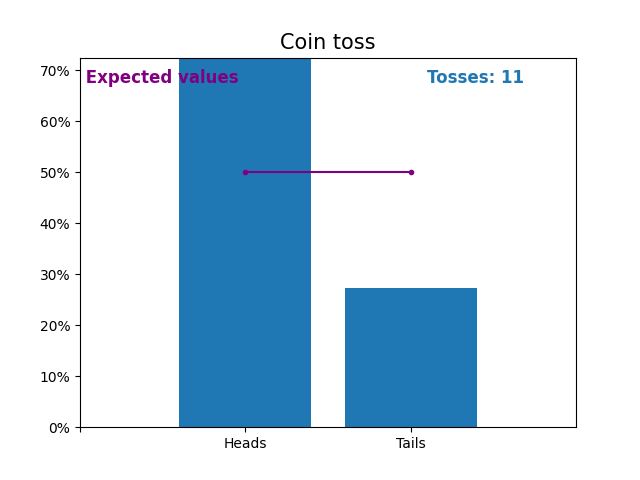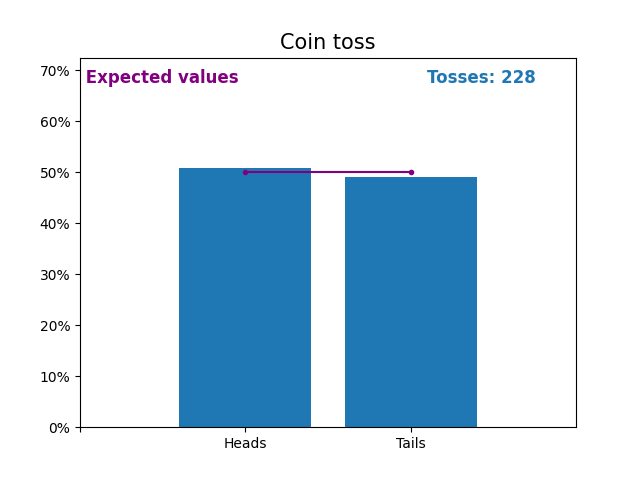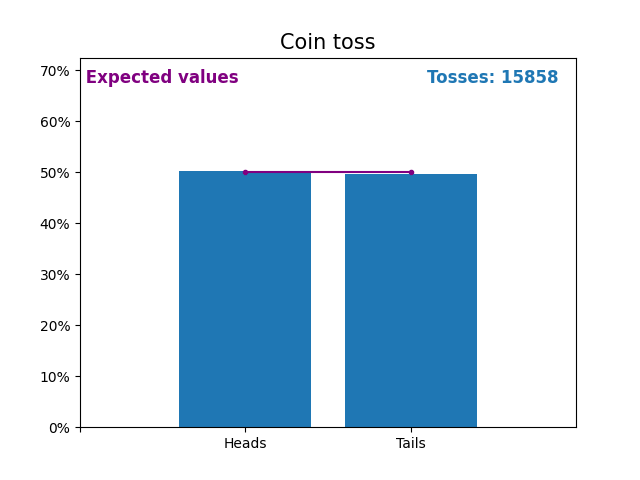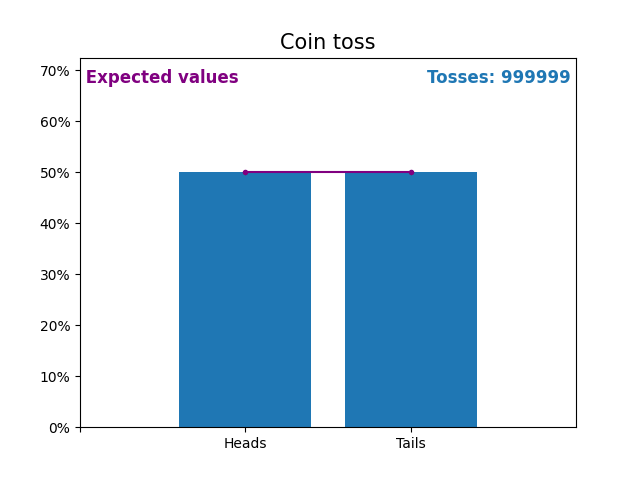
请注意，随着抛硬币次数的增加，随机抛硬币的结果如何越来越接近预期值（50%）。

同样，这是一张图，显示了掷骰子次数不断增加的结果以及预期的结果（从 1 到 6）。

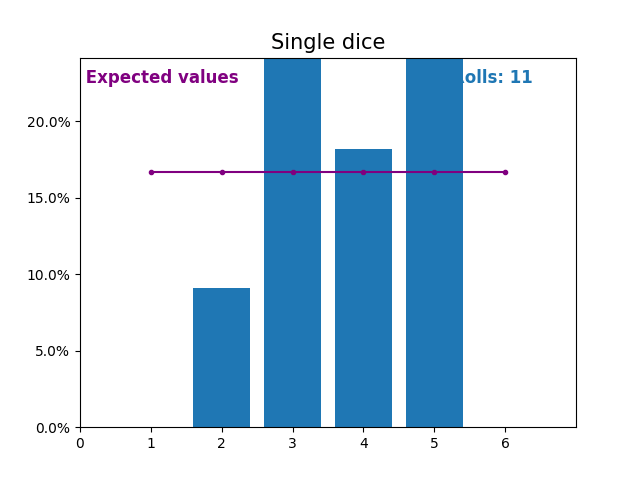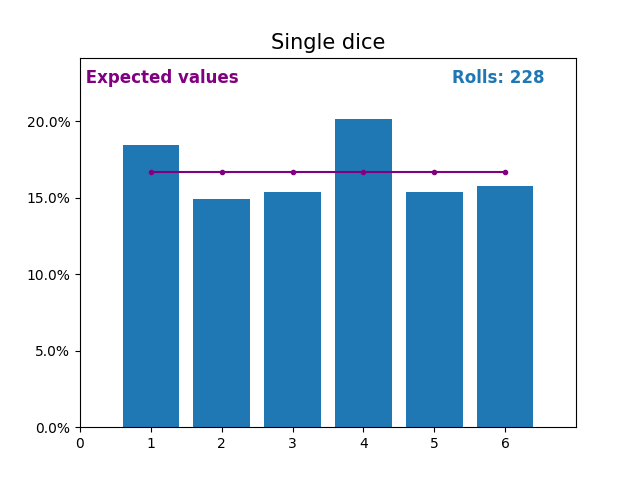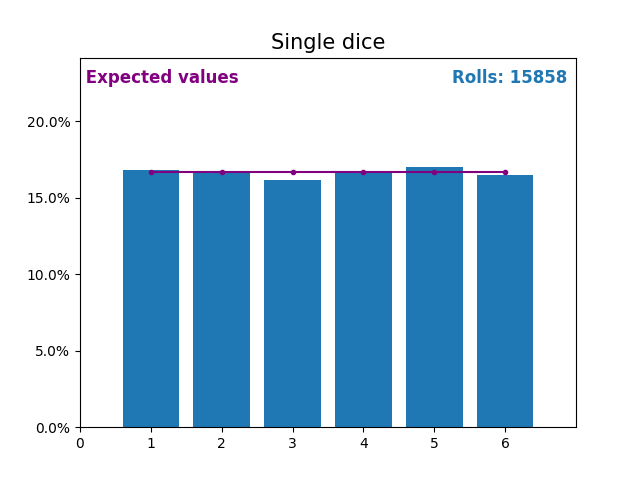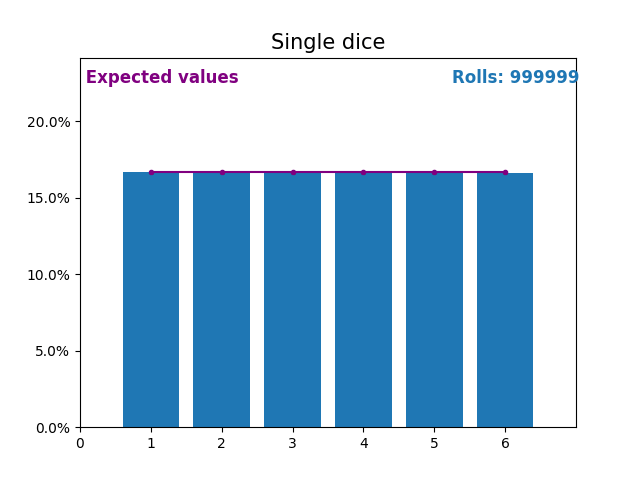
再次注意，随着掷骰子次数的增加，随机掷骰子的结果如何越来越接近预期值（1/6，或 16.666%）。

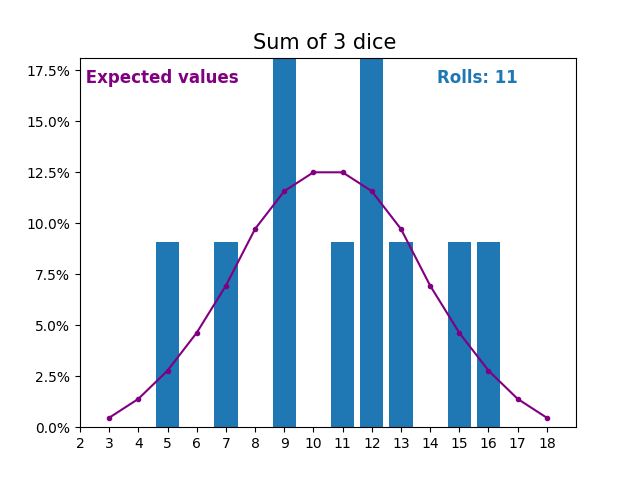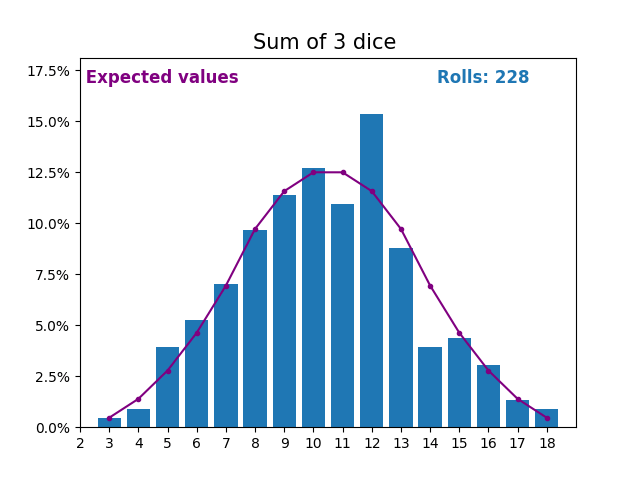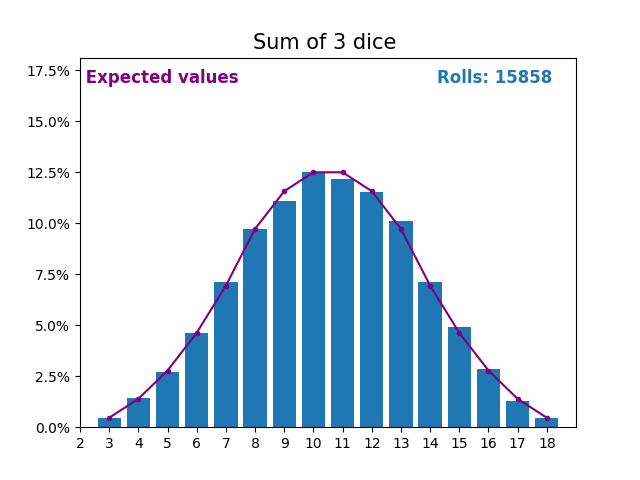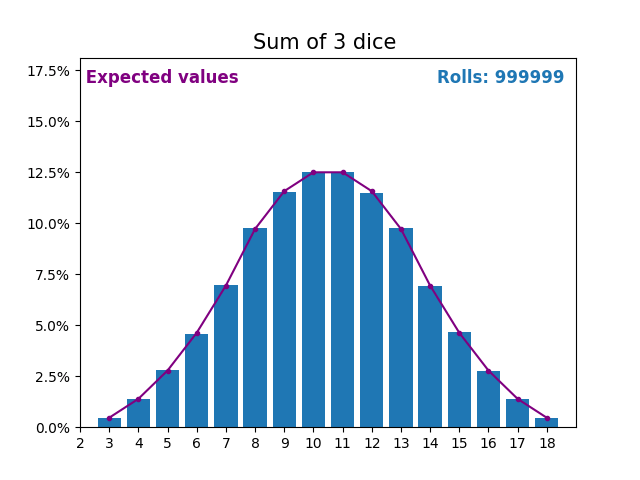
当随机变量是骰子点数之和时，结果和预期值会呈现不同的形状。

不同的形状来自于得到中间值附近的和的方式比得到小或大的和的方式更多。

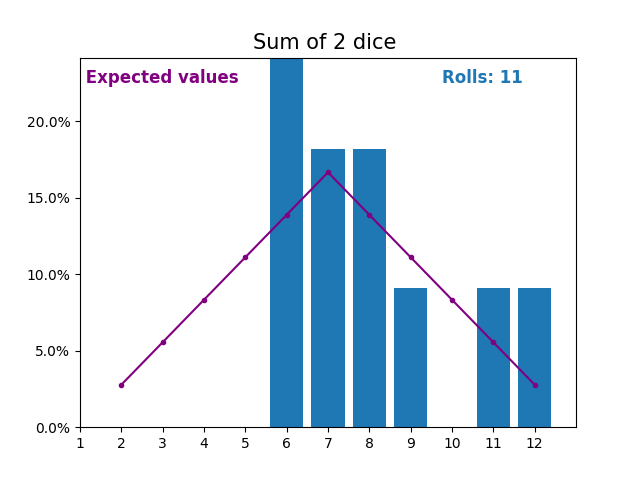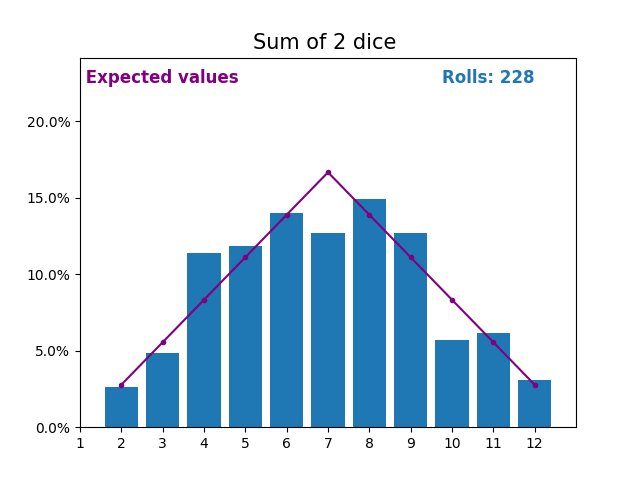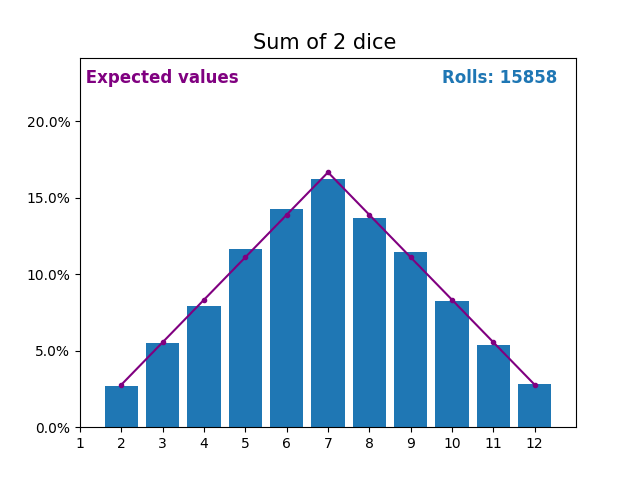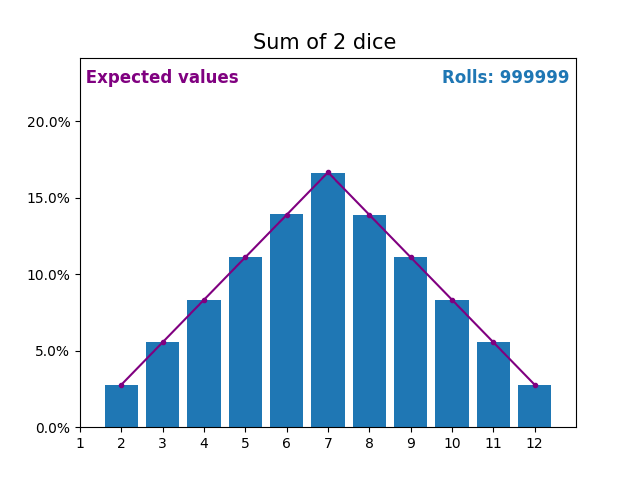
随着我们不断增加用于求和的骰子数量，结果和预期值的形状越来越像正态分布。

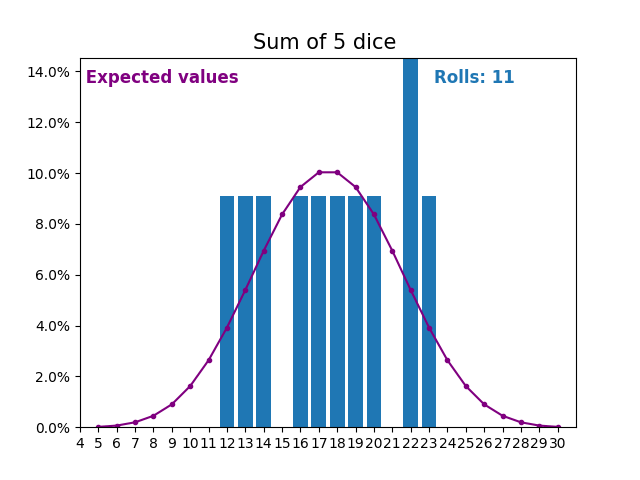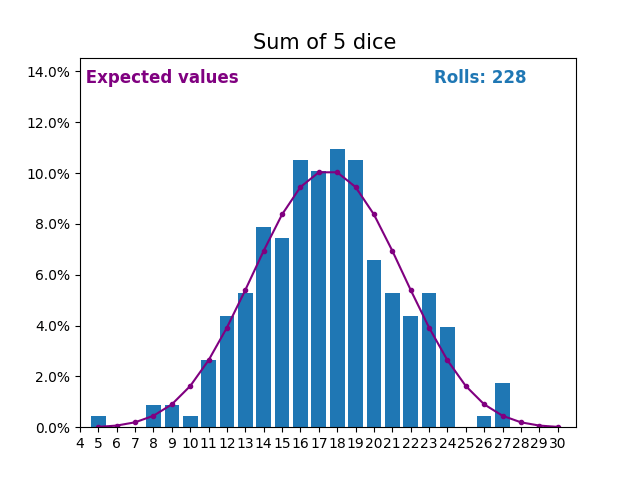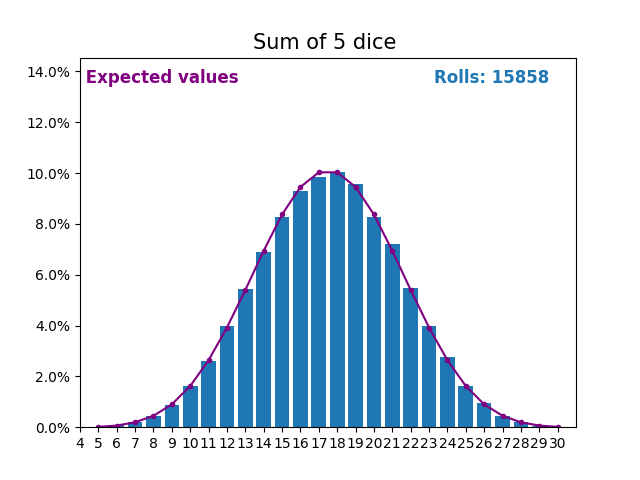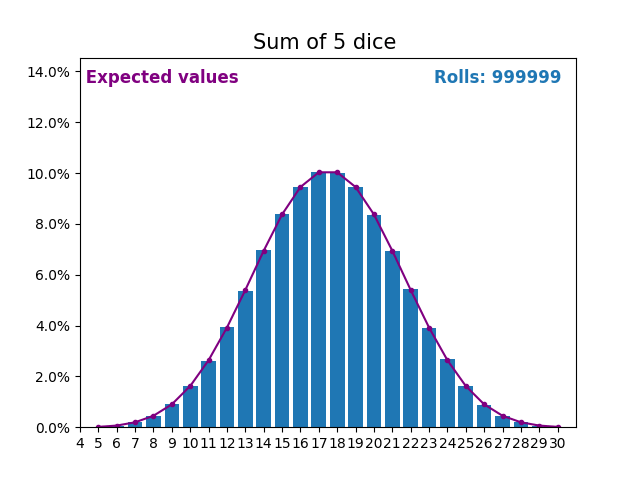
许多现实世界的变量遵循相似的模式，并自然形成正态分布。

正态分布变量可以使用众所周知的技术进行分析。

您将在接下来的几页中学习一些最常见和最有用的技术。