DSA 时间复杂度
运行时间
要完全理解算法,我们必须了解如何评估算法完成工作所需的时间,即运行时间。
探索算法的运行时间很重要,因为使用低效的算法可能会使我们的程序变慢甚至无法使用。
通过了解算法的运行时间,我们可以选择适合我们需求的算法,并且可以使我们的程序运行得更快,并有效地处理更多数据。
实际运行时间
在考虑不同算法的运行时,我们**不会**关注已实现算法实际使用的运行时间,原因如下。
如果我们在编程语言中实现一个算法,并运行该程序,那么它实际使用的运行时间将取决于许多因素
- 用于实现算法的编程语言
- 程序员如何编写算法程序
- 用于运行已实现算法的编译器或解释器
- 运行算法的计算机硬件
- 计算机上正在运行的操作系统和其他任务
- 算法正在处理的数据量
由于所有这些不同因素都影响着算法的实际运行时间,我们怎么知道一种算法是否比另一种算法更快?我们需要找到一种更好的运行时间衡量标准。
时间复杂度
为了评估和比较不同的算法,与其关注算法的实际运行时间,不如使用一种称为时间复杂度的概念更有意义。
时间复杂度比实际运行时间更抽象,并且不考虑编程语言或硬件等因素。
时间复杂度是指算法在处理大量数据时所需的运算次数。运算次数可以被视为时间,因为计算机对每次运算都使用一定的时间。
例如,在查找数组中最小值的算法中,数组中的每个值都必须比较一次。每次这样的比较都可以视为一次运算,而每次运算都需要一定的时间。因此,算法查找最小值所需的总时间取决于数组中的值的数量。
查找最小值所需的时间因此与值的数量成线性关系。100 个值需要 100 次比较,而 5000 个值需要 5000 次比较。
时间和数组中值的数量之间的关系是线性的,并可以在如下图形中显示
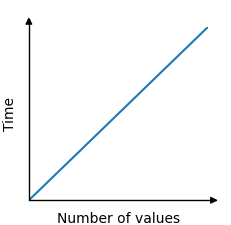
"一次运算"
当这里谈论“运算”时,“一次运算”可能需要一个或几个 CPU 周期,它只是一个帮助我们进行抽象的词,这样我们才能理解什么是时间复杂度,并找到不同算法的时间复杂度。
算法中的一次运算可以理解为我们在算法的每次迭代中或针对每个数据项执行的操作,这些操作需要恒定的时间。
例如:比较两个数组元素,如果一个比另一个大就交换它们,就像冒泡排序算法所做的那样,可以被视为一次运算。将此理解为一次、两次或三次运算,实际上并不会影响冒泡排序的时间复杂度,因为它的时间是恒定的。
我们说一个运算需要“恒定时间”,如果它花费的时间与算法处理的数据量(\(n\))无关。比较两个特定的数组元素,如果一个比另一个大就交换它们,无论数组包含 10 个还是 1000 个元素,所需的时间都相同。
大 O 符号
在数学中,大 O 符号用于描述函数的上界。
在计算机科学中,大 O 符号更具体地用于查找算法的最坏情况时间复杂度。
大 O 符号使用大写字母 O 加上括号 \(O() \),括号内有一个表达式,表示算法的运行时间。运行时间通常用 \(n \) 来表示,它是在算法处理的数据集中的值的数量。
以下是一些算法大 O 符号的示例,仅供参考
| 时间复杂度 | 算法 |
|---|---|
| \[ O(1) \] | 查找数组中的特定元素,例如 |
| \[ O(n) \] | 查找最小值。算法必须对 \(n \) 个值的数组执行 \(n \) 次运算才能找到最小值,因为算法必须将每个值比较一次。 |
| \[ O(n^2) \] |
冒泡排序、选择排序和插入排序是具有此时间复杂度的算法。它们的时间复杂度原因将在这些算法的页面中进行解释。 大型数据集会显著减慢这些算法的速度。仅将 \(n \) 从 100 增加到 200 个值,运算次数就可能增加多达 30000! |
| \[ O(n \log n) \] | 快速排序算法平均而言比上面提到的三种排序算法快,其中 \(O(n \log n) \) 是平均情况而不是最坏情况时间。快速排序的最坏情况时间也是 \(O(n^2) \),但正是平均时间使得快速排序如此有趣。我们将在稍后学习快速排序。 |
不同算法的时间随值 \(n\) 增加的变化情况如下
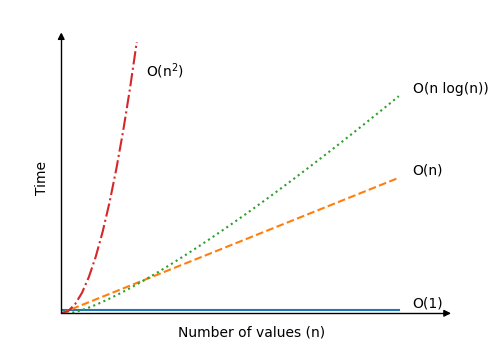
最佳、平均和最坏情况
在解释大 O 符号时已经提到了“最坏情况”时间复杂度,但算法如何会有最坏情况场景呢?
查找具有 \(n \) 个值的数组中最小值的算法需要 \(n \) 次运算才能完成,这始终是相同的。所以这个算法的最佳、平均和最坏情况场景都是相同的。
但是对于我们接下来将要研究的许多其他算法,如果我们保持值的数量 \(n \) 固定,运行时间仍然会根据实际值发生很大变化。
在不深入所有细节的情况下,我们可以理解排序算法可以有不同的运行时间,这取决于它正在排序的值。
想象一下,您必须手动将 20 个值从低到高排序
8, 16, 19, 15, 2, 17, 4, 11, 6, 1, 7, 13, 5, 3, 9, 12, 14, 20, 18, 10
这会花费您几秒钟完成。
现在,想象您必须对 20 个已经近乎排序的值进行排序
1, 2, 3, 4, 5, 20, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
您可以非常快地对这些值进行排序,只需将 20 移到列表末尾即可完成,对吧?
算法的工作方式类似:对于相同数量的数据,它们有时会慢,有时会快。因此,为了能够比较不同算法的时间复杂度,我们通常使用大 O 符号来关注最坏情况。
大 O 数学解释
根据您的数学背景,本节可能难以理解。它旨在为那些需要更全面解释大 O 的人提供更扎实的数学基础。
如果您现在不理解,请不要担心,以后可以回来。如果这里的数学内容对您来说太难了,也不用太担心,您仍然可以享受本教程中的各种算法,学习如何编程它们,并理解它们的速度快慢。
在数学中,大 O 符号用于创建函数的上界,而在计算机科学中,大 O 符号用于描述当数据值 \(n\) 增加时算法运行时间的增长方式。
例如,考虑函数
\[f(n) = 0.5n^3 -0.75n^2+1 \]
函数 \(f\) 的图如下所示
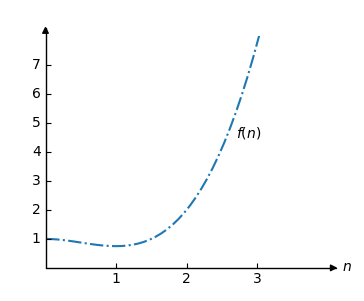
考虑另一个函数
\[g(n) = n^3 \]
我们可以将其绘制如下
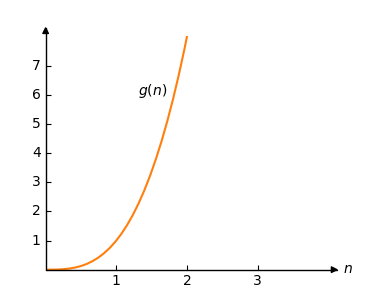
使用大 O 符号,我们可以说 \(O(g(n))\) 是 \(f(n)\) 的上界,因为我们可以选择一个常数 \(C \),使得只要 \(n \) 足够大,就有 \(C \cdot g(n)>f(n)\)。
好的,让我们试试。我们选择 \(C=0.75 \),这样 \(C \cdot g(n) = 0.75 \cdot n^3\)。
现在,让我们在同一个图中绘制 \(0.75 \cdot g(n)\) 和 \(f(n)\)
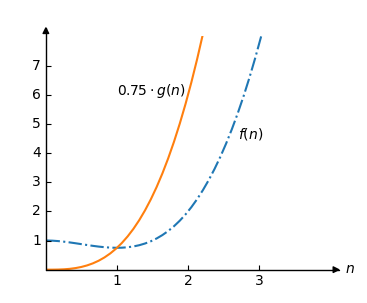
我们可以看到 \(O(g(n))=O(n^3)\) 是 \(f(n)\) 的上界,因为对于所有大于 1 的 \(n \),都有 \(0.75 \cdot g(n) > f(n)\)。
在上面的例子中,\(n\) 必须大于 1 才能使 \(O(n^3)\) 成为上界。我们将这个限制称为 \(n_0\)。
Definition(定义)
设 \(f(n)\) 和 \(g(n)\) 为两个函数。我们说 \(f(n)\) 是 \(O(g(n))\) 当且仅当存在正的常数 \(C\) 和 \(n_0\),使得
\[ C \cdot g(n) > f(n) \]
对于所有 \(n>n_0\)。
在评估算法的时间复杂度时,\(O()\)
只对大量 \(n \) 值有效是可以的,因为这正是时间复杂度变得重要的时候。换句话说:如果我们正在排序,10、20 或 100 个值,算法的时间复杂度并不是那么有趣,因为计算机无论如何都会在短时间内对这些值进行排序。

