DSA 计数排序时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

计数排序时间复杂度

计数排序的工作原理是首先计算不同值的出现次数，然后利用这些次数来按排序顺序重构数组。

经验法则是，当可能值的范围 \(k\) 小于值的数量 \(n\) 时，计数排序算法的运行速度很快。

要使用大 O 表示法表示时间复杂度，我们首先需要计算算法执行的操作数。

• 查找最大值：必须对每个值进行一次评估，以确定它是否为最大值，因此需要 \(n\) 次操作。
• 初始化计数数组：在数组中的最大值为 \(k\) 的情况下，我们需要 \(k+1\) 个元素在计数数组中，以便包含 0。计数数组中的每个元素都必须初始化，因此需要 \(k+1\) 次操作。
• 我们要排序的每个值都会被计数一次，然后删除，因此每次计数需要 2 次操作，总共 \(2 \cdot n\) 次操作。
• 构建排序数组：创建排序数组中的 \(n\) 个元素：\(n\) 次操作。

总计我们得到

\[ \begin{equation} \begin{aligned} 操作 {} & = n + (k+1) + (2 \cdot n) + n \\ & = 4 \cdot n + k + 1 \\ & \approx 4 \cdot n + k \end{aligned} \end{equation} \]

根据我们之前对时间复杂度的了解，我们可以创建一个简化的表达式，使用大 O 表示法来表示时间复杂度。

\[ \begin{equation} \begin{aligned} O(4 \cdot n + k) {} & = O(4 \cdot n) + O(k) \\ & = O(n) + O(k) \\ & = \underline{\underline{O(n+k)}} \end{aligned} \end{equation} \]

正如前面所提到的，计数排序在不同值的范围 \(k\) 相对于要排序的值的总数 \(n\) 较小时是有效的。我们现在可以直接从大 O 表达式 \(O(n+k)\) 中看出这一点。

例如，假设不同数字的范围 \(k\) 是要排序的值的数量的 10 倍。在这种情况下，我们可以看到算法花费了大部分时间来处理不同数字的范围 \(k\)，尽管要排序的实际值 \(n\) 相比较小。

对于计数排序，在图表中显示时间复杂度或进行时间复杂度模拟并不直接，因为时间复杂度受到值范围 \(k\) 的很大影响。

下面是一个图表，显示了计数排序的时间复杂度可能有多大差异，随后是对最佳和最坏情况的解释。

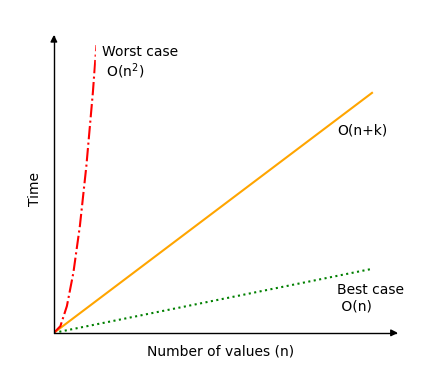
计数排序的最佳情况是范围 \(k\) 仅占 \(n\) 的一小部分，例如 \(k(n)=0.1 \cdot n\)。例如，对于 100 个值，范围是从 0 到 10；或者对于 1000 个值，范围是从 0 到 100。在这种情况下，我们得到时间复杂度 \(O(n+k)=O(n+0.1 \cdot n) = O(1.1 \cdot n)\)，简写为 \(O(n)\)。

然而，最坏情况是范围远大于输入。假设对于仅 10 个值的输入，范围在 0 到 100 之间；或者类似地，对于 1000 个值的输入，范围在 0 到 1000000 之间。在这种情况下，\(k\) 的增长相对于 \(n\) 是二次的，如下所示：\(k(n)=n^2\)，我们得到时间复杂度 \(O(n+k)=O(n+n^2)\)，简写为 \(O(n^2)\)。甚至比这更糟糕的情况也可能出现，但选择这种情况是因为它相对容易理解，而且也许并不那么不现实。

正如你所看到的，在选择计数排序作为你的算法之前，考虑值的范围与要排序的值的数量进行比较是很重要的。此外，如页面顶部所述，请记住计数排序仅适用于非负整数值。

计数排序模拟

运行计数排序的不同模拟，以了解操作次数如何在最坏情况 \(O(n^2)\)（红线）和最佳情况 \(O(n)\)（绿线）之间变化。

如前所述：如果要排序的数字值变化很大（\(k\) 大），而要排序的数字很少（\(n\) 小），则计数排序算法无效。

如果我们保持 \(n\) 和 \(k\) 固定，模拟中的“随机”、“降序”和“升序”选项会导致相同数量的操作。这是因为在这三种情况中发生的事情是相同的：设置一个计数数组，对数字进行计数，然后创建新的排序数组。