DSA 旅行商问题

旅行商问题

旅行商问题指出，你是一名推销员，必须拜访若干个城市或城镇。

除了 Held-Karp 算法（该算法非常高级且耗时，(\(O(2^n n^2)\))，此处不作描述）之外，没有其他方法可以找到最短路线，只能通过检查所有可能的路线。

这意味着解决此问题的时空复杂度为 \(O(n!)\)，即对于 6 个城市需要检查 720 条路线，对于 8 个城市必须检查 40,320 条路线，如果你需要访问 10 个城市，则需要检查超过 360 万条路线！

旅行商问题 (TSP) 是一个值得研究的问题，因为它非常实用，但又非常耗时，以至于即使在一个只有 20-30 个顶点的图中，也几乎不可能找到最短路线。

如果我们有一个有效的算法来解决旅行商问题，那么在许多领域将产生巨大的影响，例如芯片设计、车辆路径规划、电信和城市规划。

检查所有路线以解决旅行商问题

为了找到旅行商问题的最优解，我们将检查所有可能的路线，并且每次找到一条更短的路线时，我们都会将其存储起来，这样最终我们就能得到最短的路线。

优点：找到全局最短路线。

缺点：需要大量的计算，特别是对于大量城市，这意味着它非常耗时。

这种寻找问题解决方案的方式称为蛮力法。

蛮力法并非真正的算法，它只是指通过检查所有可能性来找到解决方案，通常是因为缺乏更好的方法。

正如上面所示，旅行商问题的蛮力法之所以如此耗时，是因为我们在检查所有路线，而当城市数量增加时，可能路线的数量会急剧增加。

from itertools import permutations

def calculate_distance(route, distances):
    total_distance = 0
    for i in range(len(route) - 1):
        total_distance += distances[route[i]][route[i + 1]]
    total_distance += distances[route[-1]][route[0]]
    return total_distance

def brute_force_tsp(distances):
    n = len(distances)
    cities = list(range(1, n))
    shortest_route = None
    min_distance = float('inf')
    
    for perm in permutations(cities):
        current_route = [0] + list(perm)
        current_distance = calculate_distance(current_route, distances)
        
        if current_distance < min_distance:
            min_distance = current_distance
            shortest_route = current_route
    
    shortest_route.append(0)
    return shortest_route, min_distance

distances = [
    [0, 2, 2, 5, 9, 3],
    [2, 0, 4, 6, 7, 8],
    [2, 4, 0, 8, 6, 3],
    [5, 6, 8, 0, 4, 9],
    [9, 7, 6, 4, 0, 10],
    [3, 8, 3, 9, 10, 0]
]

route, total_distance = brute_force_tsp(distances)
print("Route:", route)
print("Total distance:", total_distance)

使用贪婪算法解决旅行商问题

由于检查所有可能的路线来解决旅行商问题（如我们上面所做的）非常耗时，我们可以改为通过在每一步都前往最近的未访问城市来找到一条短路线，这要快得多。

优点：比检查所有路线的速度快得多地找到旅行商问题的解决方案。

缺点：找不到全局最短路线，它只找到一条比平均随机路线短得多的路线。

这种在旅行商问题中寻找最短路线近似值的方法，即在每一步都前往最近的未访问城市，称为贪婪算法。

正如你通过运行此模拟几次所见，找到的路线并非完全不合理。除了偶尔出现的线路交叉（尤其是在算法后期），结果路线比随机选择下一个城市所得到的路线要短得多。

def nearest_neighbor_tsp(distances):
    n = len(distances)
    visited = [False] * n
    route = [0]
    visited[0] = True
    total_distance = 0

    for _ in range(1, n):
        last = route[-1]
        nearest = None
        min_dist = float('inf')
        for i in range(n):
            if not visited[i] and distances[last][i] < min_dist:
                min_dist = distances[last][i]
                nearest = i
        route.append(nearest)
        visited[nearest] = True
        total_distance += min_dist

    total_distance += distances[route[-1]][0]
    route.append(0)
    return route, total_distance

distances = [
    [0, 2, 2, 5, 9, 3],
    [2, 0, 4, 6, 7, 8],
    [2, 4, 0, 8, 6, 3],
    [5, 6, 8, 0, 4, 9],
    [9, 7, 6, 4, 0, 10],
    [3, 8, 3, 9, 10, 0]
]

route, total_distance = nearest_neighbor_tsp(distances)
print("Route:", route)
print("Total distance:", total_distance)

其他找到旅行商问题近似最优解的算法

除了使用贪婪算法解决旅行商问题之外，还有其他算法可以找到最短路线的近似值。

这些算法很受欢迎，因为它们比实际检查所有可能的解决方案更有效，但与上述贪婪算法一样，它们找不到全局最短路线。

用于找到旅行商问题近似最优解的算法包括：

• 2-opt 启发式算法：一种逐步改进解决方案的算法，在每一步移除两条边，然后以不同的方式重新连接两条路径，以减少总路径长度。
• 遗传算法：这是一种受自然选择过程启发的算法类型，它使用选择、变异和交叉等技术来进化问题的解决方案，包括 TSP。
• 模拟退火：这种方法受到了冶金学中退火过程的启发。它包括加热然后缓慢冷却材料以减少缺陷。在 TSP 的上下文中，它通过以允许偶尔移动到更差解决方案的方式探索解决方案空间来寻找近似最优解，这有助于避免陷入局部最小值。
• 蚁群优化：该算法受到蚂蚁在寻找从蚁群到食物源的路径的行为的启发。它是一种更复杂的概率技术，用于解决可以映射到在图中寻找良好路径的计算问题。

解决旅行商问题的时间复杂度

为了快速获得近似最优解，我们可以使用一种贪婪算法，该算法在每一步都只前往最近的未访问城市，如本页的第二个模拟所示。

以这种贪婪方式解决旅行商问题意味着，在每一步，都会将当前城市到所有其他未访问城市之间的距离进行比较，因此我们得到的时间复杂度为 \(O(n^2) \)。

但找到所有路线中最短的路线需要更多的操作，其时间复杂度为 \(O(n!)\)，如前所述，这意味着对于 4 个城市，有 4! 条可能路线，等于 \(4 \cdot 3 \cdot 2 \cdot 1 = 24\)。而对于例如仅 12 个城市，则有 \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) 条可能路线！

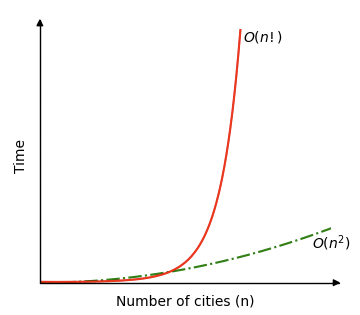
在下面的图中，可以看到贪婪算法 \(O(n^2)\) 的时间复杂度与通过比较所有路线 \(O(n!)\) 来找到最短路线的时间复杂度之间的比较。

但是，我们可以做两件事来减少需要检查的路线数量。

在旅行商问题中，路线从同一点开始和结束，形成一个环。这意味着最短路线的长度无论从哪个城市开始都将是相同的。这就是为什么我们在上面的模拟中选择了一个固定的起始城市，这使得可能路线的数量从 \(n!\) 减少到 \((n-1)!\)。

此外，由于这些路线是环形的，所以一条路线向一个方向走和向另一个方向走的距离是相同的，所以我们实际上只需要检查一半路线的距离，因为另一半只是相同的路线反向走，所以我们需要检查的路线数量实际上是 \( \frac{(n-1)!}{2}\)。

但是，即使我们可以将需要检查的路线数量减少到 \( \frac{(n-1)!}{2}\)，时间复杂度仍然是 \( O(n!)\)，因为对于非常大的 \(n\)，将 \(n\) 减一并除以 2，在 \(n\) 增加时，并不会显著改变时间复杂度的增长方式。

要更好地理解时间复杂度如何工作，请访问此页面。

实际的旅行商问题更复杂

在这个旅行商问题的上下文中，图中的边权重告诉我们从一个点到另一个点的难易程度，而我们要最小化的是一条路线的总边权重。

到目前为止，本页中的边权重一直是两个点之间的直线距离。这使得解释旅行商问题和显示它变得容易得多。

但在现实世界中，有许多其他因素会影响边权重

1. 障碍物：在从一个地方移动到另一个地方时，我们通常会试图避开障碍物，例如树木、河流、房屋。这意味着从 A 到 B 的路程更长、花费的时间更多，需要增加边权重值来考虑这一点，因为不再是直线了。
2. 交通网络：旅行时我们通常会沿着道路行驶或使用公共交通系统，这也影响了从一个地方到另一个地方的难易程度（或发送包裹）。
3. 交通状况：旅行拥堵也会影响旅行时间，因此也应该反映在边权重值中。
4. 法律和政治边界：例如，跨越边境可能会使一条路线比另一条路线更难选择，这意味着最短的直线路线可能更慢或成本更高。
5. 经济因素：使用燃料、员工时间、维护车辆，所有这些都会花费金钱，也应计入边权重。

如你所见，仅使用直线距离作为边权重可能比实际问题过于简单。并且对于这种简化的模型解决旅行商问题，可能会得到一个在实际意义上并非最优的解决方案。

当边长度不再仅仅是两个点之间的直线距离时，可视化旅行商问题并不容易，但计算机可以很好地处理这个问题。