DSA 基数排序时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

基数排序时间复杂度

基数排序算法一次对非负整数进行一位排序。

需要排序的值有 \(n\) 个，而 \(k\) 是最高值中的位数。

当基数排序运行时，每个值都会被移入基数数组，然后再移回初始数组。所以 \(n\) 个值被移入基数数组，\(n\) 个值被移回。这给了我们 \(n + n = 2 \cdot n\) 次操作。

而上述移动值的操作需要针对每一位数字进行。这使得我们总共有 \(2 \cdot n \cdot k\) 次操作。

这使得基数排序的时间复杂度为

\[ O(2 \cdot n \cdot k) = \underline{\underline{O(n \cdot k)}} \]

只要位数 \(k\) 相对于值的数量 \(n\) 保持相对较小，基数排序可能是最快的排序算法之一。

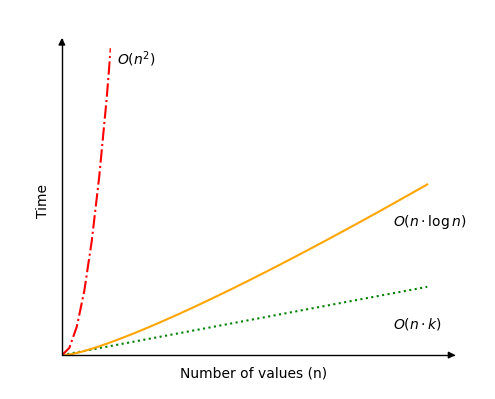
我们可以设想一种情况，即位数 \(k\) 与值的数量 \(n\) 相同，在这种情况下，我们得到时间复杂度 \(O(n \cdot k)=O(n^2)\)，这相当慢，并且与冒泡排序等算法具有相同的时间复杂度。

我们还可以设想一种情况，即位数 \(k\) 随着值的数量 \(n\) 的增长而增长，即 \(k(n)= \log n\)。在这种情况下，我们得到时间复杂度 \(O(n \cdot k)=O(n \cdot \log n )\)，这与快速排序等算法相同。

参见下图中的基数排序时间复杂度。

基数排序模拟

运行不同的基数排序模拟，以了解操作次数如何落在最坏情况 \(O(n^2)\)（红线）和最佳情况 \(O(n)\)（绿线）之间。

表示不同值的条形被缩放以适应窗口，使其看起来正常。这意味着具有 7 位数的值看起来只比具有 2 位数的值大 5 倍，但实际上，具有 7 位数的值实际上比具有 2 位数的值大 5000 倍！

如果我们保持 \(n\) 和 \(k\) 固定，上面模拟中的“随机”、“降序”和“升序”选项会导致相同数量的操作。这是因为在所有三种情况下都会发生相同的事情。