DSA 冒泡排序

冒泡排序

冒泡排序是一种将数组从最小值排序到最大值的算法。

运行模拟以查看冒泡排序算法如何对一组值进行排序。数组中的每个值都由一个列表示。

“冒泡”这个词来源于这种算法的工作方式，它使最高值“冒”到顶部。

继续阅读以完全理解冒泡排序算法以及如何自行实现它。

手动演练

在我们用编程语言实现冒泡排序算法之前，让我们先手动遍历一个短数组一次，只是为了了解其思想。

步骤 1：我们从一个未排序的数组开始。

步骤 2： 我们看前两个值。最小值在前吗？是的，所以我们不需要交换它们。

步骤 3： 向前一步，看看值 12 和 9。最小值在前吗？不是。

步骤 4： 所以我们需要交换它们，使 9 排在前面。

步骤 5： 向前一步，看看 12 和 11。

步骤 6： 我们必须交换，使 11 在 12 之前。

步骤 7： 看看 12 和 3，我们需要交换它们吗？是的。

步骤 8： 交换 12 和 3，使 3 排在前面。

运行下面的模拟以查看上述 8 个步骤的动画

手动运行：发生了什么？

我们必须理解第一次遍历中发生的事情，才能完全理解该算法，从而可以用编程语言实现它。

您能看出最高值 12 发生了什么吗？它已经冒到数组的末尾，也就是它所属的位置。但数组的其余部分仍未排序。

因此，冒泡排序算法必须一次又一次地遍历数组，每次下一个最高值都会冒到其正确位置。排序一直持续到最小值 3 留在数组的开头。这意味着我们需要遍历数组 4 次，才能对 5 个值的数组进行排序。

每次算法遍历数组时，数组中剩余的未排序部分都会变短。

这就是一次完整的手动遍历的样子

我们现在将利用所学知识，用编程语言实现冒泡排序算法。

冒泡排序实现

要在编程语言中实现冒泡排序算法，我们需要

1. 一个包含待排序值的数组。
2. 一个内部循环，它遍历数组并在第一个值高于下一个值时交换值。此循环每次运行时必须少遍历一个值。
3. 一个外部循环，它控制内部循环必须运行的次数。对于一个包含 n 个值的数组，此外部循环必须运行 n-1 次。

生成的代码如下：

my_array = [64, 34, 25, 12, 22, 11, 90, 5]

n = len(my_array)
for i in range(n-1):
    for j in range(n-i-1):
        if my_array[j] > my_array[j+1]:
            my_array[j], my_array[j+1] = my_array[j+1], my_array[j]

print("Sorted array:", my_array)

冒泡排序改进

冒泡排序算法可以再改进一点。

想象一下数组几乎已经排序，最低的数字在开头，例如这样：

my_array = [7, 3, 9, 12, 11]

在这种情况下，数组在第一次运行后就会被排序，但冒泡排序算法会继续运行，而不会交换元素，这是不必要的。

如果算法一次遍历数组而没有交换任何值，那么数组必须已完成排序，我们可以停止算法，像这样：

my_array = [7, 3, 9, 12, 11]

n = len(my_array)
for i in range(n-1):
    swapped = False
    for j in range(n-i-1):
        if my_array[j] > my_array[j+1]:
            my_array[j], my_array[j+1] = my_array[j+1], my_array[j]
            swapped = True
    if not swapped:
        break

print("Sorted array:", my_array)

冒泡排序时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关冒泡排序时间复杂度的更深入和详细解释，请访问 此页面。

冒泡排序算法遍历数组中的每个值，将其与相邻值进行比较。因此，对于一个包含 \(n\) 个值的数组，在一个循环中必须有 \(n\) 次这样的比较。

在一个循环之后，数组会再次循环遍历 \(n\) 次。

这意味着总共进行了 \(n \cdot n\) 次比较，因此冒泡排序的时间复杂度为

\[ \underline{\underline{O(n^2)}} \]

描述冒泡排序时间复杂度的图表如下所示

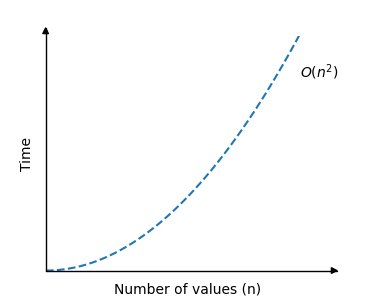
如您所见，当数组大小增加时，运行时间会非常快地增加。

幸运的是，还有比这更快的排序算法，例如我们稍后会看到的快速排序。

您可以在下方模拟冒泡排序，其中红色虚线是理论时间复杂度 \(O(n^2)\)。您可以选择值的数量 \(n\)，并运行实际的冒泡排序实现，其中操作被计数，并且计数在下面的图中标记为蓝色十字。理论与实践相比如何？

[,,,,]