DSA 线性搜索时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

线性搜索时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关插入排序时间复杂度的更全面、详细的解释，请访问 此页面。

线性搜索 将每个值与要查找的值进行比较。如果找到该值，则返回其索引；如果未找到，则返回 -1。

要找出线性搜索的时间复杂度，让我们看看在包含 \(n\) 个值的数组中查找值所需的比较操作次数。

最佳情况场景是，如果我们正在查找的值是数组中的第一个值。在这种情况下，只需一次比较，时间复杂度为 \(O(1)\)。

最坏情况场景是，在不找到目标值的情况下，整个数组都被搜索过。在这种情况下，数组中的所有值都与目标值进行了比较，时间复杂度为 \(O(n)\)。

平均情况场景并不容易确定。找到目标值的可能性有多大？这取决于数组中的值，对吧？但如果我们假设数组中的一个值等于目标值，并且该值的位置可以是任意的，那么线性搜索所需的平均时间是比最坏情况场景所需时间的一半。

线性搜索的时间复杂度为 \(O(n)\)。

如果我们绘制线性搜索在包含 \(n\) 个值的数组中查找值所需时间的图表，我们会得到这个图：

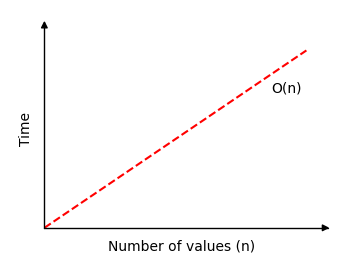
线性搜索模拟

运行不同数量值的数组的模拟，看看线性搜索找到 \(n\) 个值数组中的值需要多少次比较。

正如你在运行线性搜索模拟时所看到的，如果值很快就被找到，搜索只需要很少的比较，但如果我们正在寻找的值没有被找到，那么就会进行最多的比较。