DSA 特定算法的时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

快速排序时间复杂度

快速排序算法选择一个值作为“枢轴”元素，并将其他值移动，使大于枢轴的值位于枢轴元素的右侧，小于枢轴的值位于枢轴元素的左侧。

然后，快速排序算法通过递归地对枢轴元素左右两侧的子数组进行排序，直到数组被排序。

最坏情况

要找到快速排序的时间复杂度，我们可以从最坏情况开始分析。

快速排序的最坏情况是数组已经排序。在这种情况下，每次递归调用后只有一个子数组，并且新子数组比前一个数组短一个元素。

这意味着快速排序必须递归调用自身 \(n\) 次，并且每次都必须进行 \(\frac{n}{2}\) 次平均比较。

最坏情况时间复杂度为：

\[ O(n \cdot \frac{n}{2}) = \underline{\underline{O(n^2)}} \]

平均情况

平均而言，快速排序实际上要快得多。

快速排序在平均情况下速度很快，因为每次快速排序递归运行时，数组大约被分成两半，所以子数组的大小减小得非常快，这意味着不需要太多递归调用，并且快速排序可以比最坏情况更快地完成。

下图显示了用快速排序对包含 23 个值的数组进行排序时，数组是如何被分成子数组的。

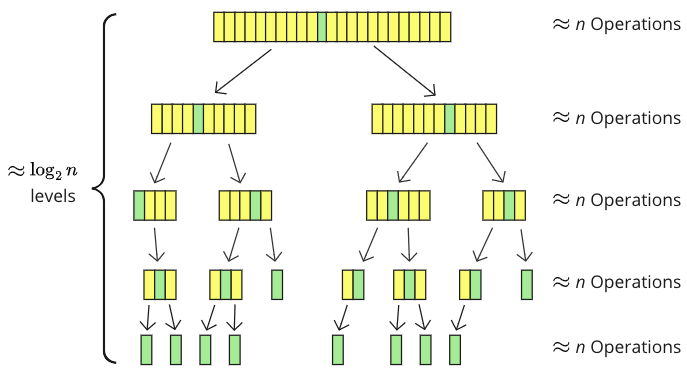
枢轴元素（绿色）被移到中间，数组被分成子数组（黄色）。有 5 个递归级别，子数组越来越小，每个级别大约有 \(n\) 个值以某种方式被触及：比较、移动或两者都进行。

\( \log_2 \) 表示一个数字可以分成 2 的次数，所以 \( \log_2 \) 是递归级别的数量的一个很好的估计。 \( \log_2(23) \approx 4.5 \)，这对于上面具体示例中的递归级别数量来说是一个足够好的近似值。

实际上，子数组并不总是精确地分成两半，并且每个级别并不总是比较或移动 \(n\) 个值，但我们可以说这是计算时间复杂度的平均情况。

\[ \underline{\underline{O(n \cdot \log_2n)}} \]

下面您可以看到与之前的排序算法（冒泡排序、选择排序和插入排序）相比，快速排序在平均情况下的时间复杂度的显著改进。

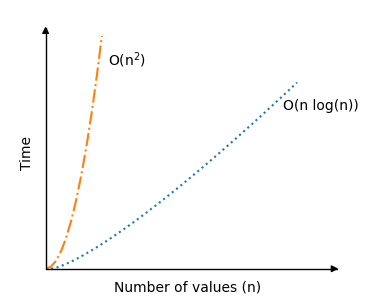
快速排序算法的递归部分实际上是平均排序场景如此之快的原因，因为对于枢轴元素的良好选择，数组将在算法每次调用自身时大致均匀地分成两半。因此，即使 \(n\) 的数量翻倍，递归调用的次数也不会翻倍。

快速排序模拟

使用下面的模拟来查看理论时间复杂度 \(O(n^2)\)（红线）与实际快速排序运行的操作数量的比较。

上图中的红线代表最坏情况下的理论上限时间复杂度 \(O(n^2)\)，绿线代表具有随机值的平均情况时间复杂度 \(O(n \log_2n)\)。

对于快速排序，平均随机情况和已排序数组的情况之间存在很大差异。您可以通过运行上面的不同模拟来看到这一点。

升序排序的数组需要大量操作的原因在于，由于其实现方式，它需要最多的元素交换。在这种情况下，选择最后一个元素作为枢轴元素，而最后一个元素也是最大的数字。因此，每个子数组中的所有其他值都会被交换到枢轴元素的左侧（它们已经位于该位置）。