DSA 冒泡排序时间复杂度

有关时间复杂度的通用解释，请参阅上一页。

冒泡排序时间复杂度

冒泡排序算法在最坏情况下需要对长度为 \(n\) 的数组进行 \(n-1\) 次遍历。

第一次遍历时，算法会将每个元素与下一个元素进行比较，如果左边的值大于右边的值，则交换它们。这意味着最大的值会“冒泡”到最后，并且未排序的数组部分会越来越短，直到排序完成。因此，在平均情况下，当算法遍历数组进行比较和交换值时，会考虑 \(\frac{n}{2}\) 个元素。

我们可以开始计算冒泡排序算法对 \(n\) 个值的操作次数：

\[操作次数 = (n-1)\cdot \frac{n}{2} = \frac{n^2}{2} - \frac{n}{2} \]

在考虑算法的时间复杂度时，我们关注非常大的数据集，这意味着 \(n\) 是一个非常大的数字。对于一个非常大的数字 \(n\)，\(\frac{n^2}{2}\) 项会比 \(\frac{n}{2}\) 项大得多。大到我们可以通过简单地移除第二项 \(\frac{n}{2}\) 来进行近似。

\[操作次数 = \frac{n^2}{2} - \frac{n}{2} \approx \frac{n^2}{2} = \frac{1}{2} \cdot n^2 \]

当我们在这里使用大 O 符号来分析时间复杂度时，因子会被忽略，因此 \(\frac{1}{2}\) 这个因子会被省略。这意味着冒泡排序算法的运行时间可以使用大 O 符号来描述，如下所示：

\[ O( \frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]

描述冒泡排序时间复杂度的图如下所示：

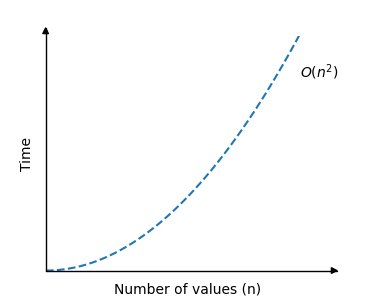
正如你所见，当数组大小增加时，运行时间会非常快地增加。

幸运的是，有一些排序算法比它更快，例如 快速排序。

冒泡排序模拟

选择数组中的元素数量，然后运行此模拟，以了解冒泡排序处理 \(n\) 个元素的数组所需的操作次数 \(O(n^2)\)。

上方的红线表示上限时间复杂度 \(O(n^2)\)，而此时的实际函数是 \(1.05 \cdot n^2\)。

如果存在一个正常量 \(C\)，使得对于大量的 \(n\) 值，\(C \cdot g(n) > f(n)\)，则称函数 \(f(n)\) 为 \(O(g(n))\)。

在这种情况下，\(f(n)\) 是冒泡排序使用的操作数，\(g(n)=n^2\)，\(C=1.05\)。

在此页面上阅读更多关于大 O 符号和时间复杂度的信息。