DSA 基数排序

基数排序

基数排序算法通过对数组中的每个数字进行排序来完成，从最低有效位（最右边的位）开始。

基数（或底数）是数字系统中唯一数字的数量。在我们通常使用的十进制系统中，从 0 到 9 有 10 个不同的数字。

基数排序使用基数，将十进制值放入 10 个不同的桶（或容器）中，这些桶与当前关注的数字相对应，然后在移动到下一个数字之前，再将它们放回数组中。

基数排序是一种非比较算法，仅适用于非负整数。

基数排序算法可以描述如下：

稳定排序

基数排序必须以稳定方式对元素进行排序，结果才能正确排序。

稳定的排序算法是一种在排序前后保持相同值元素顺序的算法。假设我们有两个元素 "K" 和 "L"，其中 "K" 排在 "L" 前面，它们的值都为 "3"。如果元素 "K" 在数组排序后仍然排在 "L" 前面，则该排序算法被认为是稳定的。

对于我们之前单独研究过的算法，讨论稳定排序算法意义不大，因为无论它们是否稳定，结果都是相同的。但对于基数排序来说，确保在每个数字位置上进行稳定排序非常重要，因为元素一次只按一个数字进行排序。

因此，在对最低有效位上的元素进行排序并移动到下一个数字时，重要的是不要破坏之前数字位置上已完成的排序工作，这就是为什么我们需要确保基数排序以稳定方式对每个数字位置进行排序。

在下面的模拟中，我们将揭示如何进行底层排序到桶中。为了更好地理解稳定排序的工作原理，您还可以选择以不稳定方式排序，这将导致不正确的结果。通过简单地从数组的末尾而不是开头将元素放入桶中，可以使排序不稳定。

手动演练

让我们手动尝试排序，以便在用编程语言实现基数排序之前，更好地理解它的工作原理。

步骤 1：我们从一个未排序的数组开始，以及一个空的数组来容纳具有相应基数 0 到 9 的值。

步骤 2：我们开始按关注的最低有效位进行排序。

步骤 3：现在，我们将元素根据关注的数字移动到基数数组中的正确位置。元素从 myArray 的开头获取，并推送到 radixArray 的正确位置。

步骤 4：我们将元素移回初始数组，现在对最低有效位进行了排序。元素从 radixArray 的末尾获取，并放入 myArray 的开头。

步骤 5：我们转移焦点到下一个数字。请注意，值 45 和 25 仍然保持它们开始时的相对顺序，因为我们以稳定方式排序。

步骤 6：根据关注的数字，我们将元素移入基数数组。

步骤 7：我们将元素从 radixArray 的末尾移回 myArray 的开头。

排序完成！

运行下面的模拟，以动画形式查看以上步骤。

手动运行：发生了什么？

我们看到值从数组移出，并根据当前关注的基数放入基数数组中。然后，这些值又被移回我们要排序的数组中。

这种从要排序的数组中移出值然后又移回的操作，必须执行的次数等于值中最大数字的数量。例如，如果数组中需要排序的最高数字是 437，那么我们知道必须排序三次，一次处理一个数字。

我们还看到，基数数组需要是二维的，以便可以容纳具有特定基数或索引的多个值。

而且，如前所述，我们必须以一种保持具有相同关注基数的值的顺序的方式在两个数组之间移动值，这样排序才是稳定的。

基数排序实现

为了实现基数排序算法，我们需要：

1. 一个需要排序的非负整数数组。
2. 一个索引从 0 到 9 的二维数组，用于存储当前关注基数的值。
3. 一个循环，将值从未排序的数组中取出，并将其放置在二维基数数组的正确位置。
4. 一个循环，将值从基数数组移回初始数组。
5. 一个外循环，其运行次数等于最高值中的数字数量。

生成的代码如下：

myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixArray = [[], [], [], [], [], [], [], [], [], []]
maxVal = max(myArray)
exp = 1

while maxVal // exp > 0:

    while len(myArray) > 0:
        val = myArray.pop()
        radixIndex = (val // exp) % 10
        radixArray[radixIndex].append(val)

    for bucket in radixArray:
        while len(bucket) > 0:
            val = bucket.pop()
            myArray.append(val)

    exp *= 10

print("Sorted array:", myArray)

在第 7 行，我们使用地板除法（"//"）将最大值 802 除以 1，这是 while 循环第一次运行时。下一次除以 10，最后一次除以 100。使用地板除法（"//"）时，将忽略小数点后的任何数字，并返回一个整数。

在第 11 行，根据值的基数（关注的数字）决定将其放置在 radixArray 中的哪个位置。例如，外层 while 循环第二次运行时，exp 将是 10。值 170 除以 10 将得到 17。"%10" 操作将 17 除以 10 一次，余数为 7。所以值 170 被放入 radixArray 的索引 7。

使用其他排序算法的基数排序

基数排序实际上可以与任何其他排序算法一起实现，只要该算法是稳定的。这意味着，当涉及到按特定数字排序时，任何稳定的排序算法都可以工作，例如计数排序或冒泡排序。

这是使用冒泡排序对单个数字进行排序的基数排序实现。

def bubbleSort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                
def radixSortWithBubbleSort(arr):
    max_val = max(arr)
    exp = 1
    
    while max_val // exp > 0:
        radixArray = [[],[],[],[],[],[],[],[],[],[]]
        
        for num in arr:
            radixIndex = (num // exp) % 10
            radixArray[radixIndex].append(num)
        
        for bucket in radixArray:
            bubbleSort(bucket)
        
        i = 0
        for bucket in radixArray:
            for num in bucket:
                arr[i] = num
                i += 1
        
        exp *= 10

myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixSortWithBubbleSort(myArray)
print("Sorted array:", myArray)

基数排序时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关基数排序时间复杂度的更全面和详细的解释，请访问 此页面。

基数排序的时间复杂度是

\[ \underline{\underline{O(n \cdot k)}} \]

这意味着基数排序既取决于需要排序的值的数量 \(n\)，也取决于最高值 \(k\) 中的数字数量。

基数排序的最佳情况是，如果要排序的值很多，但这些值只有很少的数字。例如，如果要排序的值超过一百万，而最高值是 999，只有三个数字。在这种情况下，时间复杂度 \(O(n \cdot k)\) 可以简化为 \(O(n)\)。

基数排序的最坏情况是，最高值中的数字数量与要排序的值的数量相同。这可能不是一种常见情况，但这种情况下时间复杂度将是 \(O(n^2)\)。

最平均或最常见的情况可能是，数字的数量 \(k\) 类似于 \(k(n)= \log n\)。如果是这样，基数排序的时间复杂度将是 \(O(n \cdot \log n )\)。这种情况的一个例子是，如果要排序 1000000 个值，而这些值有 6 位数字。

请参见下图所示的基数排序的不同可能时间复杂度。

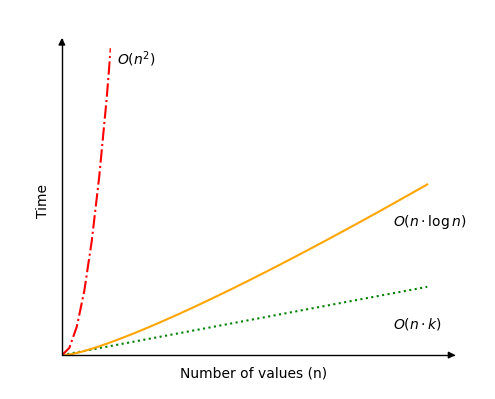
运行基数排序的不同模拟，以查看操作次数在最坏情况 \(O(n^2)\)（红线）和最佳情况 \(O(n)\)（绿线）之间如何变化。

代表不同值的条形被缩放到适合窗口，使其看起来还可以。这意味着具有 7 位数字的值看起来只比具有 2 位数字的值大 5 倍，但实际上，具有 7 位数字的值实际上比具有 2 位数字的值大 5000 倍！

如果我们保持 \(n\) 和 \(k\) 固定，模拟中的“随机”、“降序”和“升序”选项会产生相同数量的操作。这是因为这三种情况都会发生相同的事情。

Radix Sort must use a  
sorting algorithm.