DSA 计数排序

计数排序

计数排序算法通过计算每个值出现的次数来对数组进行排序。

运行模拟，看看如何使用计数排序对 1 到 5 之间的 17 个整数值进行排序。

计数排序不像我们之前看过的其他排序算法那样进行值比较，它只适用于非负整数。

此外，当可能值的范围 \(k\) 小于值的数量 \(n\) 时，计数排序非常快。

计数排序的条件

这些是计数排序被认为仅适用于有限范围的非负整数值的原因

• 整数值：计数排序依赖于对不同值出现次数的计数，因此它们必须是整数。对于整数，每个值都可以与一个索引匹配（对于非负值），并且存在有限数量的不同值，因此可能的不同值 \(k\) 的数量不会比值的数量 \(n\) 大太多。
• 非负值：计数排序通常通过创建计数数组来实现。当算法遍历需要排序的值时，通过增加计数数组中索引 x 处的值来计算值 x。如果我们尝试对负值进行排序，那么对于值 -3，我们会遇到麻烦，因为索引 -3 将在计数数组之外。
• 值的范围有限：如果可能要排序的不同值的数量 \(k\) 大于要排序的值的数量 \(n\)，那么我们排序所需的计数数组将大于我们拥有的需要排序的原始数组，算法会变得无效。

手动演练

在用编程语言实现计数排序算法之前，让我们手动遍历一个短数组，以便先了解其思路。

步骤 1：我们从一个未排序的数组开始。

步骤 2：我们创建另一个数组来统计每个值的数量。该数组有 4 个元素，用于存储 0 到 3 的值。

步骤 3：现在我们开始计数。第一个元素是 2，所以我们必须将计数数组索引 2 处的元素加一。

步骤 4：计数完一个值后，我们可以将其移除，然后计数下一个值，即 3。

步骤 5：我们计数的下一个值是 0，所以我们将计数数组索引 0 处的元素加一。

步骤 6：我们继续这样做，直到所有值都被计数。

步骤 7：现在我们将从初始数组中重新创建元素，并且我们将按从小到大的顺序进行。

计数数组中的第一个元素告诉我们有一个值为 0 的元素。因此，我们将一个值为 0 的元素添加到数组中，并将计数数组索引 0 处的元素减一。

步骤 8：从计数数组中，我们看到我们不需要创建值为 1 的元素。

步骤 9：我们将 3 个值为 2 的元素添加到数组末尾。在我们创建这些元素的同时，我们也减少了计数数组索引 2 处的值。

步骤 10：最后，我们必须在数组末尾添加 2 个值为 3 的元素。

终于！数组已排序。

运行下面的模拟，以动画形式查看以上步骤。

手动运行：发生了什么？

在用编程语言实现算法之前，我们需要更详细地回顾一下上面发生的事情。

我们已经看到计数排序算法分两个步骤进行

1. 每个值都通过在计数数组的正确索引处递增来计数。计数完一个值后，它就会被移除。
2. 值通过使用计数数组中的计数和计数索引，以正确的顺序重新创建。

有了这个想法，我们就可以开始使用 Python 来实现算法了。

计数排序实现

要在编程语言中实现计数排序算法，我们需要

1. 一个包含待排序值的数组。
2. 一个接收整数数组的“countingSort”方法。
3. 方法内部的一个数组，用于保存值的计数。
4. 方法内部的一个循环，通过递增计数数组中的元素来计数和移除值。
5. 方法内部的一个循环，通过使用计数数组来重新创建数组，使元素按正确的顺序出现。

还有一件事：我们需要找出数组中的最大值，这样计数数组才能以正确的尺寸创建。例如，如果最大值为 5，那么计数数组必须总共有 6 个元素，才能计数所有可能的非负整数 0、1、2、3、4 和 5。

生成的代码如下：

def countingSort(arr):
    max_val = max(arr)
    count = [0] * (max_val + 1)

    while len(arr) > 0:
        num = arr.pop(0)
        count[num] += 1

    for i in range(len(count)):
        while count[i] > 0:
            arr.append(i)
            count[i] -= 1

    return arr

unsortedArr = [4, 2, 2, 6, 3, 3, 1, 6, 5, 2, 3]
sortedArr = countingSort(unsortedArr)
print("Sorted array:", sortedArr)

计数排序时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关插入排序时间复杂度的更全面详细的解释，请访问此页面。

计数排序算法的运行速度取决于可能值的范围 \(k\) 和值的数量 \(n\)。

总的来说，计数排序的时间复杂度为 \(O(n+k)\)。

在最佳情况下，可能的不同值的范围 \(k\) 相对于值的数量 \(n\) 非常小，计数排序的时间复杂度为 \(O(n)\)。

但在最坏的情况下，可能的不同值的范围 \(k\) 相对于值的数量 \(n\) 非常大，计数排序的时间复杂度可能为 \(O(n^2)\) 甚至更糟。

下面的图显示了计数排序的时间复杂度可能变化多大。

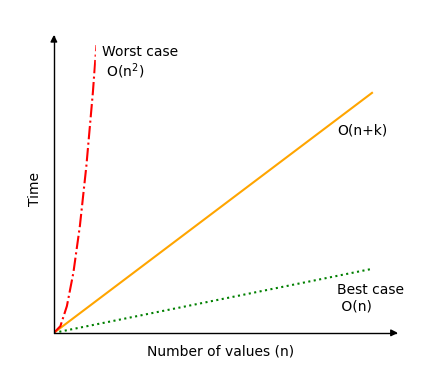
如您所见，在选择计数排序作为算法之前，考虑值的范围与要排序的值的数量进行比较非常重要。另外，正如页面顶部提到的，请记住，计数排序仅适用于非负整数值。

运行计数排序的不同模拟，以查看操作次数如何落在最坏情况 \(O(n^2)\)（红线）和最佳情况 \(O(n)\)（绿线）之间。

如前所述：如果待排序的数字值差异很大（\(k\) 很大），而要排序的数字很少（\(n\) 很小），则计数排序算法效果不佳。

如果我们保持 \(n\) 和 \(k\) 固定，“随机”、“降序”和“升序”选项在上面的模拟中导致的操作次数相同。这是因为在这三种情况下都会发生相同的事情：设置计数数组，对数字进行计数，然后创建新的排序后的数组。

[,,,4,2,1]