DSA 快速排序

快速排序

顾名思义，快速排序是最快的排序算法之一。

快速排序算法接受一个值数组，选择其中一个值作为“枢轴”元素，然后移动其他值，使得较小的值位于枢轴元素的左侧，较大的值位于其右侧。

在本教程中，我们选择数组的最后一个元素作为枢轴元素，但我们也可以选择数组的第一个元素，或者实际上是数组中的任何元素。

然后，快速排序算法递归地对枢轴元素左右两侧的子数组执行相同的操作。这会一直持续到数组被排序。

该算法可以描述为：

请继续阅读，以全面了解快速排序算法以及如何自己实现它。

手动演练

在我们用编程语言实现快速排序算法之前，让我们手动地遍历一个简短的数组，以便了解其原理。

步骤 1：我们从一个未排序的数组开始。

步骤 2：我们选择最后一个值 3 作为枢轴元素。

步骤 3：数组中的其余值都大于 3，并且必须在 3 的右侧。将 3 和 11 交换。

步骤 4：值 3 现在处于正确的位置。我们需要对 3 右侧的值进行排序。我们选择最后一个值 11 作为新的枢轴元素。

步骤 5：值 7 必须位于枢轴值 11 的左侧，而 12 必须位于其右侧。移动 7 和 12。

步骤 6：将 11 和 12 交换，以便较小的值 9 和 7 位于 11 的左侧，而 12 位于右侧。

步骤 7：11 和 12 处于正确的位置。我们选择 7 作为子数组 [ 9, 7] 中 11 左侧的枢轴元素。

步骤 8：我们必须交换 9 和 7。

现在，数组已排序。

运行下面的模拟，以动画形式查看以上步骤。

手动运行：发生了什么？

在我们用编程语言实现算法之前，需要更详细地回顾一下上面发生的事情。

我们已经知道数组的最后一个值被选为枢轴元素，而其余值被排列成小于枢轴值的值在左侧，大于枢轴值的值在右侧。

之后，枢轴元素与较高值中的第一个元素交换。这会将原始数组分成两部分，枢轴元素位于较低值和较高值之间。

现在，我们需要对旧枢轴元素左右两侧的子数组执行相同的操作。如果子数组的长度为 0 或 1，我们则认为它已排序。

总而言之，快速排序算法使子数组越来越短，直到数组被排序。

快速排序实现

为了编写一个 'quickSort' 方法来将数组分割成越来越短的子数组，我们使用递归。这意味着 'quickSort' 方法必须用枢轴元素左右两侧的新子数组来调用自身。在此处阅读有关递归的更多信息：此处。

要在编程语言中实现快速排序算法，我们需要：

1. 一个包含待排序值的数组。
2. 一个 quickSort 方法，如果子数组的大小大于 1，它会调用自身（递归）。
3. 一个 partition 方法，它接收一个子数组，移动值，将枢轴元素交换到子数组中，并返回下一个子数组分割发生的位置索引。

生成的代码如下：

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        quicksort(array, low, pivot_index-1)
        quicksort(array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)

快速排序时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关快速排序时间复杂度的更全面、详细的解释，请访问此页面。

快速排序的最坏情况是 \(O(n^2) \)。这是因为枢轴元素是每个子数组中的最高值或最低值，这会导致大量递归调用。使用我们上面的实现，当数组已经排序时就会发生这种情况。

但平均而言，快速排序的时间复杂度实际上只有 \(O(n \log n) \)，这比我们之前看过的排序算法要好得多。这就是快速排序如此受欢迎的原因。

在下面的模拟中，您可以看到快速排序在平均场景 \(O(n \log n) \) 下的时间复杂度与之前排序算法（冒泡排序、选择排序和插入排序）的时间复杂度 \(O(n^2) \) 相比有了显著的提高。

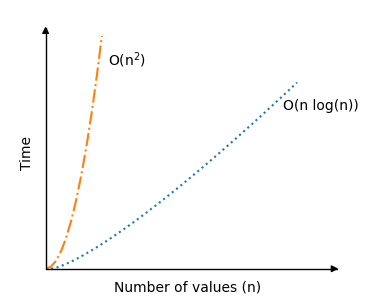
快速排序算法的递归部分实际上是平均排序场景之所以如此快速的原因，因为如果枢轴元素选择得当，数组每次调用算法时都会大致平均地分成两半。因此，即使值的数量 \(n \) 加倍，递归调用的次数也不会加倍。

在下面的模拟中，使用不同数量的值和不同类型的数组运行快速排序。

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        (array, low, pivot_index-1)
        (array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)