DSA 选择排序时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

二分查找时间复杂度

二分查找 通过检查中间值来在已排序的数组中查找目标值。如果中间值不是目标值，则线性搜索会选择左侧或右侧的子数组，并继续搜索，直到找到目标值。

要找到二分查找的时间复杂度，让我们看看在具有 \(n\) 个值的数组中查找目标值需要多少次比较操作。

最佳情况是第一个中间值与目标值相同。如果发生这种情况，目标值会立即找到，只需一次比较，因此在这种情况下时间复杂度为 \(O(1)\)。

最坏情况是搜索区域必须反复减半，直到搜索区域只剩下一个值。发生这种情况时，无论是否找到目标值，都不会影响时间复杂度。

我们来考虑长度为 2 的幂的数组，例如 2、4、8、16、32、64 等。

在将 2 除以二直到我们只看到一个值之前，需要多少次？只需要一次，对吧？

那 8 呢？我们需要将一个 8 个值的数组减半 3 次才能得到一个值。

一个 32 个值的数组必须减半 5 次。

我们可以看到 \(2=2^1\)，\(8=2^3\)，\(32=2^5\)。因此，我们需要减半数组多少次才能得到一个元素，可以在以 2 为底的幂中找到。另一种看待它的方式是问“我必须将 2 乘以自身多少次才能得到这个数字？”。在数学上，我们可以使用以 2 为底的对数，这样我们就可以发现长度为 \(n\) 的数组可以被分成 \( \log_{2}(n)\) 次。

这意味着二分查找的时间复杂度是

\[ \underline{\underline{O( \log_{2} n )}} \]

平均情况并不那么容易确定，但是由于我们使用大 O 表示法将算法的时间复杂度视为最坏情况的上限，因此平均情况并没有那么有趣。

如果我们绘制二分查找在具有 \(n\) 个值的数组中查找值所需的时间与线性查找的比较图，我们将得到这个图

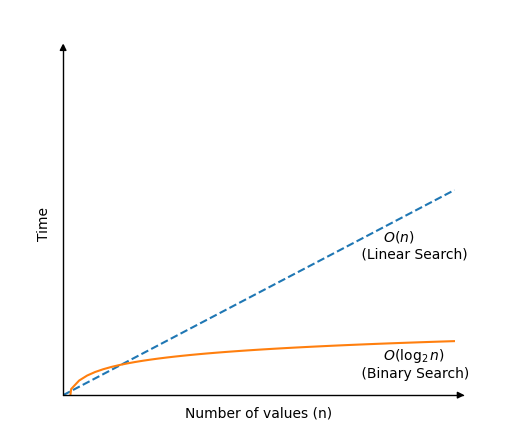
二分查找模拟

运行不同数量值 \(n\) 的数组的模拟，看看二分查找找到目标值需要多少次比较

正如您在运行二分查找模拟时所看到的，即使数组很大并且我们正在寻找的值未找到，搜索也只需要很少的比较。