DSA 合并排序时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

合并排序时间复杂度

Merge Sort 算法将数组分解成越来越小的片段。

当子数组被合并回一起，并且最小的值排在前面时，数组就会被排序。

需要排序的数组有 \(n\) 个值，我们可以通过查看算法所需的 the number of operations 来找到时间复杂度。

Merge Sort 主要的操作是分割，然后通过比较元素来进行合并。

为了将数组从头开始分割，直到子数组只包含一个值，Merge Sort 总共需要 \(n-1\) 次分割。想象一个包含 16 个值的数组。它被分割一次成长度为 8 的子数组，再次分割，再分割，子数组的大小减小到 4、2，最后是 1。对于一个 16 个元素的数组，分割次数是 \(1+2+4+8=15\)。

下图显示了对包含 16 个数字的数组需要 15 次分割。

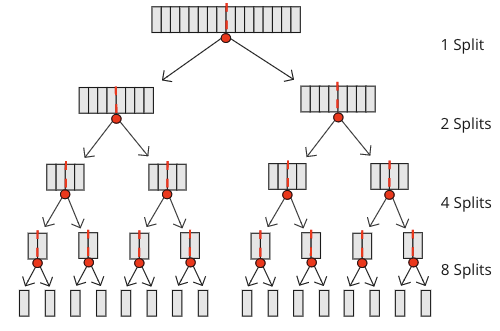
合并的次数实际上也是 \(n-1\) 次，与分割次数相同，因为每次分割都需要一次合并来重建数组。每次合并时，都会对子数组中的值进行比较，以便合并结果是有序的。

在合并两个子数组时，生成最多比较的 worst case scenario 是子数组大小相等。考虑合并 [1,4,6,9] 和 [2,3,7,8]。在这种情况下，需要进行以下比较：

1. 比较 1 和 2，结果：[1]
2. 比较 4 和 2，结果：[1,2]
3. 比较 4 和 3，结果：[1,2,3]
4. 比较 4 和 7，结果：[1,2,3,4]
5. 比较 6 和 7，结果：[1,2,3,4,6]
6. 比较 9 和 7，结果：[1,2,3,4,6,7]
7. 比较 9 和 8，结果：[1,2,3,4,6,7,8]

在合并结束时，只有一个数组中还剩下值 9，另一个数组为空，因此不需要比较就可以将最后一个值放入，合并后的数组是 [1,2,3,4,6,7,8,9]。我们看到合并 8 个值（每个初始子数组 4 个值）需要 7 次比较。总的来说，在 worst case scenario 中，合并 \(n\) 个值需要 \(n-1\) 次比较。

为了简化，我们假设合并 \(n\) 个值需要 \(n\) 次比较而不是 \(n-1\) 次。当 \(n\) 很大时，这可以接受，因为我们想使用 Big O 符号计算一个上限。

因此，在每个合并发生的层级，需要 \(n\) 次比较，有多少层呢？好吧，对于 \(n=16\)，我们有 \(n=16=2^4\)，所以有 4 层合并。对于 \(n=32=2^5\)，有 5 层合并，每层需要 \(n\) 次比较。对于 \(n=1024=2^{10}\)，需要 10 层合并。要找出 2 的多少次方等于 1024，我们使用以 2 为底的对数。答案是 10。数学上看起来是这样的：\( \log_{2}1024=10\)。

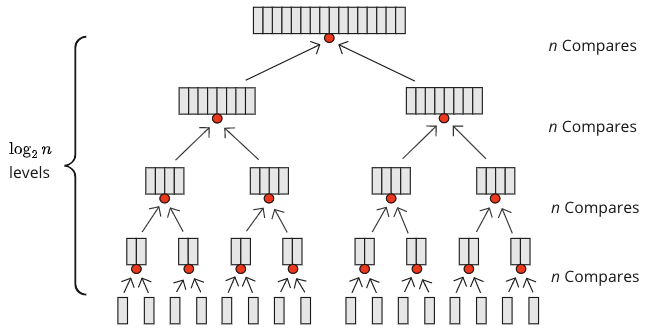
正如我们在上面的图表中看到的，每层需要 \(n\) 次比较，并且有 \( \log_{2}n\) 层，所以总共有 \( n \cdot \log_{2}n\) 次比较操作。

时间复杂度可以根据分割操作次数和合并操作次数来计算。

\[ \begin{equation} \begin{aligned} O( (n-1) + n \cdot \log_{2}n) {} & = O( n \cdot \log_{2}n ) \end{aligned} \end{equation} \]

分割操作次数 \((n-1)\) 可以从上面的 Big O 计算中移除，因为对于大的 \(n\)，\( n \cdot \log_{2}n\) 将占主导地位，并且这是我们计算算法时间复杂度的方式。

下图显示了当 Merge Sort 在一个具有 \(n\) 个值的数组上运行时，时间是如何增加的。

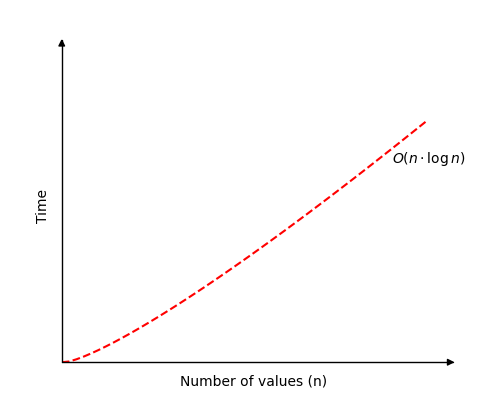
与其他许多排序算法相比，Merge Sort 的最好和最坏情况之间的差异并不大。

Merge Sort 模拟

运行模拟，尝试不同的数组值数量，看看 Merge Sort 在一个包含 \(n\) 个元素的数组上需要的操作次数 \(O(n \log n)\)

如果我们将值的数量 \(n\) 固定，"随机"、"降序"和"升序"所需的操作数量几乎相同。

Merge Sort 每次执行的性能几乎相同，因为数组被分割和合并（使用比较），无论数组是否已排序。