DSA 插入排序时间复杂度

有关时间复杂度的通用解释，请参阅此页面。

插入排序时间复杂度

插入排序最坏情况的场景是数组已经排序，但数值是从大到小排列的。这是因为在这种情况下，每个新值都必须“穿过”整个已排序的数组部分。

以下是插入排序算法为前几个元素执行的操作：

• 第 1 个值已在正确的位置。
• 第 2 个值必须与第 1 个值进行比较并移到其后。
• 第 3 个值必须与前面两个值进行比较并移到它们之后。
• 第 3 个值必须与前面三个值进行比较并移到它们之后。
• 以此类推……

如果我们继续这种模式，那么对于 \(n\) 个值，总操作次数为：

\[1+2+3+...+(n-1)\]

这是数学中一个众所周知的数列，可以写成：

\[ \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2} \]

对于非常大的 \(n\)，\(\frac{n^2}{2}\) 项占主导地位，因此我们可以通过移除第二项 \(\frac{n}{2}\) 来简化。

使用大 O 符号，插入排序算法的时间复杂度为：

\[ O(\frac{n^2}{2}) = O(\frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]

时间复杂度可以显示如下：

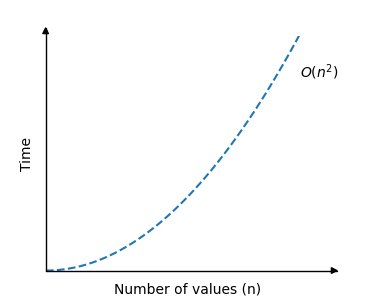
如您所见，当值 \(n\) 增加时，插入排序使用的时间会快速增加。

插入排序模拟

使用下面的模拟来查看理论时间复杂度 \(O(n^2)\)（红线）与实际插入排序操作次数的比较。

对于插入排序，最佳、平均和最坏情况场景之间存在很大差异。您可以通过运行上面的不同模拟来查看。

上面的红线代表理论上的上限时间复杂度 \(O(n^2)\)，而实际函数是 \(1.07 \cdot n^2\)。

请记住，如果存在一个正常量 \(C\) 使得 \(C \cdot g(n)>f(n)\)，则称函数 \(f(n)\) 为 \(O(g(n))\)。

在这种情况下，\(f(n)\) 是插入排序使用的操作数，\(g(n)=n^2\)，而 \(C=1.07\)。