DSA 线性搜索

线性搜索

线性搜索算法通过数组进行搜索，并返回所搜索值的索引。

运行上面的模拟，查看线性搜索算法的工作原理。

要查看值未找到时会发生什么，请尝试查找值 5。

这种算法非常简单，易于理解和实现。

如果数组已经排序，最好使用我们将在下一页介绍的、速度快得多的二分搜索算法。

排序算法和搜索算法之间的一个大区别是，排序算法会修改数组，而搜索算法会保持数组不变。

手动演练

在实际用编程语言实现线性搜索之前，我们先手动尝试一下，以便更好地理解其工作原理。我们将搜索值 11。

第一步： 我们从一个随机值数组开始。

第二步： 我们查看数组中的第一个值，它是否等于 11？

第三步： 我们移动到索引 1 处的下一个值，并将其与 11 进行比较，看它们是否相等。

第四步： 我们检查索引 2 处的下一个值。

第五步： 我们移动到索引 3 处的下一个值。它是否等于 11？

我们找到了！

值 11 在索引 3 处找到。

返回索引位置 3。

线性搜索完成。

运行下面的模拟，以动画形式查看以上步骤。

手动运行：发生了什么？

这个算法非常直接。

从数组开头开始检查每个值，看该值是否等于 11（我们要查找的值）。

找到该值后，搜索停止，并返回找到该值的索引。

如果遍历整个数组都没有找到该值，则返回 -1。

线性搜索实现

要实现线性搜索算法，我们需要

1. 一个包含要搜索值的数组。
2. 要搜索的目标值。
3. 一个从头到尾遍历数组的循环。
4. 一个 if 语句，用于比较当前值与目标值，如果找到目标值，则返回当前索引。
5. 循环结束后，返回 -1，因为此时我们知道目标值未找到。

线性搜索的结果代码如下所示：

def linearSearch(arr, targetVal):
    for i in range(len(arr)):
        if arr[i] == targetVal:
            return i
    return -1

arr = [3, 7, 2, 9, 5]
targetVal = 9

result = linearSearch(arr, targetVal)

if result != -1:
    print("Value",targetVal,"found at index",result)
else:
    print("Value",targetVal,"not found")

线性搜索时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关插入排序时间复杂度的更全面、详细的解释，请访问 此页面。

如果线性搜索运行并找到目标值，并且目标值是 \(n\) 个值的数组中的第一个数组值，则只需要一次比较。

但是，如果线性搜索遍历完 \(n\) 个值的整个数组而没有找到目标值，则需要 \(n\) 次比较。

这意味着线性搜索的时间复杂度为：

\[ O(n) \]

如果我们绘制线性搜索在 \(n\) 个值的数组中查找值所需的时间图，我们会得到这张图：

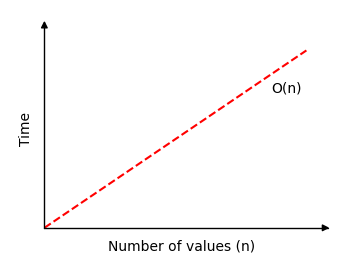
运行下面的模拟，尝试不同的数组大小，看看线性搜索需要多少次比较才能在 \(n\) 个值的数组中找到一个值。

在上面的模拟中选择“随机”、“降序”或“升序”对线性搜索的速度没有影响。

def linearSearch(arr, targetVal):
    for i in range(len(arr)):
        if arr[i] == targetVal:
          
    return -1