DSA 插入排序

插入排序

插入排序算法使用数组的一部分来存储已排序的值，另一部分存储尚未排序的值。

算法一次从数组的未排序部分取出一个值，并将其放到已排序部分数组中的正确位置，直到数组被排序。

继续阅读，以完全理解插入排序算法以及如何自己实现它。

手动演练

在用编程语言实现插入排序算法之前，我们先手动走一遍一个短数组，以便获得一些概念。

步骤 1：我们从一个未排序的数组开始。

步骤 2: 我们可以将第一个值视为数组的初始排序部分。如果只有一个值，那它肯定是有序的，对吧？

步骤 3: 下一个值 12 现在应该移动到已排序部分数组中的正确位置。但是 12 大于 7，所以它已经在正确的位置上。

步骤 4: 考虑下一个值 9。

步骤 5: 值 9 现在必须移动到已排序部分数组中的正确位置，所以我们将 9 放在 7 和 12 之间。

步骤 6: 下一个值是 11。

步骤 7: 我们将其移到已排序部分数组中的 9 和 12 之间。

步骤 8: 要插入到正确位置的最后一个值是 3。

步骤 9: 我们将 3 放在所有其他值的前面，因为它是最低的值。

最终，数组已排序。

运行下面的模拟，以动画形式查看以上步骤。

手动运行：发生了什么？

我们必须理解上面发生的一切，才能完全理解该算法，以便我们能够用编程语言实现该算法。

第一个值被视为数组的初始排序部分。

第一个值之后的所有值都必须与算法已排序部分中的值进行比较，以便将其插入到正确的位置。

插入排序算法必须遍历数组 4 次，以排序包含 5 个值的数组，因为我们不必对第一个值进行排序。

每次算法遍历数组时，数组中剩余的未排序部分都会变短。

我们现在将使用我们学到的知识来实现编程语言中的插入排序算法。

插入排序实现

要在编程语言中实现插入排序算法，我们需要

1. 一个包含待排序值的数组。
2. 一个外层循环，用于选择一个要排序的值。对于一个包含 \(n\) 个值的数组，这个外层循环跳过第一个值，并且必须运行 \(n-1\) 次。
3. 一个内层循环，用于遍历已排序部分数组，以找到要插入该值的位置。如果要排序的值位于索引 \(i\) 处，则数组的已排序部分从索引 \(0\) 开始，到索引 \(i-1\) 结束。

生成的代码如下：

my_array = [64, 34, 25, 12, 22, 11, 90, 5]

n = len(my_array)
for i in range(1,n):
    insert_index = i
    current_value = my_array.pop(i)
    for j in range(i-1, -1, -1):
        if my_array[j] > current_value:
            insert_index = j
    my_array.insert(insert_index, current_value)

print("Sorted array:", my_array)

插入排序改进

插入排序可以进一步改进。

上面代码中先删除一个值然后将其插入到另一个位置的方式是很直观的。例如，如果你用手牌来做插入排序，你就会这样做。如果将低数值的牌按顺序排在左边，你拿起一张新的未排序的牌，然后将其插入到已排序牌的正确位置。

这种编程方式的问题在于，当从数组中删除一个值时，所有上面的元素都必须向下移动一个索引位

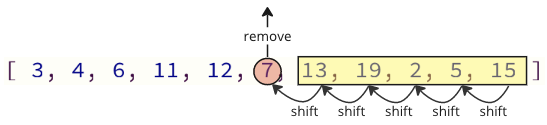
并且当再次将移除的值插入到数组中时，也有许多移位操作必须完成：所有后续元素都必须向上移动一个位置，以为插入的值腾出空间

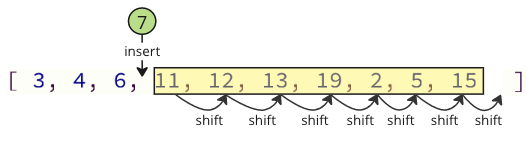
这些移位操作可能会花费大量时间，特别是对于包含许多元素的数组。

改进的解决方案

我们可以通过只移动必要的值来避免大部分的移位操作

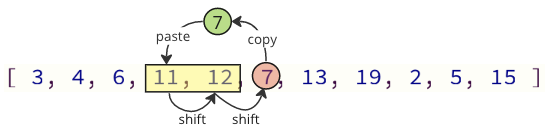
在上面的图中，首先复制了值 7，然后将值 11 和 12 向上移动一位，最后将值 7 放在原来值 11 的位置。

在这种情况下，移位操作的数量从 12 减少到 2。

下面的示例实现了这一改进

my_array = [64, 34, 25, 12, 22, 11, 90, 5]

n = len(my_array)
for i in range(1,n):
    insert_index = i
    current_value = my_array[i]
    for j in range(i-1, -1, -1):
        if my_array[j] > current_value:
            my_array[j+1] = my_array[j]
            insert_index = j
        else:
            break
    my_array[insert_index] = current_value

print("Sorted array:", my_array)

上面的代码中还做了在找到当前值的正确位置后跳出内层循环。这是因为当找到当前值的正确位置后，就没有必要继续比较其他值了。

插入排序时间复杂度

有关时间复杂度的一般性解释，请访问此页面。

有关插入排序时间复杂度的更全面、详细的解释，请访问 此页面。

选择排序对 \(n\) 个值的数组进行排序。

平均而言，每个值必须与大约 \(\frac{n}{2}\) 个其他值进行比较，才能确定将其插入到何处。

并且选择排序的循环必须大约运行 \(n\) 次才能将值插入到其正确的位置。

我们得到插入排序的时间复杂度

\[ O( \frac{n}{2} \cdot n) = \underline{\underline{O(n^2)}} \]

插入排序的时间复杂度可以显示如下

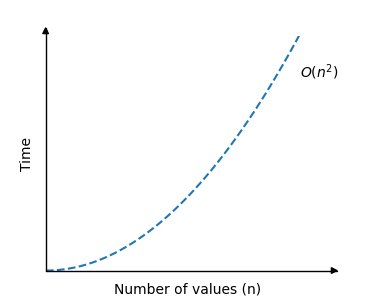
使用下面的模拟来查看理论时间复杂度 \(O(n^2)\)（红线）与实际插入排序操作次数的比较。

对于插入排序，最佳、平均和最坏情况场景之间存在很大差异。您可以通过运行上面的不同模拟来查看。

接下来是快速排序。我们终于将看到一个更快的排序算法了！