向量

向量表示法

向量有多种写法。最常见的是

或

几何中的向量

左图是向量。 长度显示大小。 箭头显示方向。

运动

向量是运动的基本组成部分

在几何学中，向量可以描述从一个点到另一个点的移动。

向量 [3, 2] 表示向右移动 3 个单位，向上移动 2 个单位。

向量加法

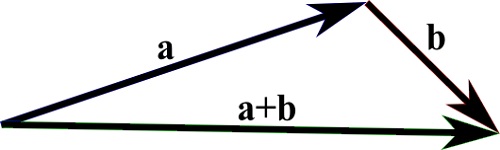
两个向量 (a+b) 的和是通过将向量 b 移动到向量 a 的头部，使其尾部与向量 a 的头部相遇而找到的。（这不会改变向量 b）。

然后，从 a 的尾部到 b 的头部的连线就是向量 a+b

向量减法

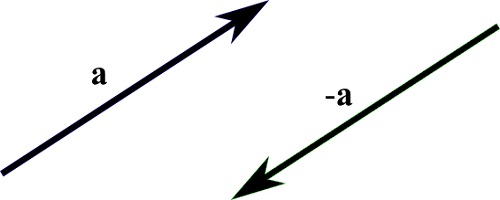
向量 -a 是 +a 的相反。

这意味着向量 a 和向量 -a 在相反方向上具有相同的大小

标量运算

向量可以通过将标量（数字）加、减或乘以所有向量值来修改

a = [1 1 1]

a + 1 = [2 2 2]

[1 2 3] + 1 = [2 3 4]

向量乘法与普通乘法具有许多相同的性质

[2 2 2] * 3 = [6 6 6]

[6 6 6] / 3 = [2 2 2]

力

力是向量。

力是具有大小和方向的向量。

速度

速度是向量。

速度是具有大小和方向的向量。