张量
Tensor 是一个 N 维矩阵
- Scalar 是一个 0 维张量
- Vector 是一个 1 维张量
- Matrix 是一个 2 维张量
Tensor 是 Vectors 和 Matrices 向更高维度推广的泛化。
| 标量 | 向量 | ||||||||||||||||||||||||||
| 1 |
|
||||||||||||||||||||||||||
| 矩阵 | 张量 | ||||||||||||||||||||||||||
|
|
Tensor 的秩
Tensor 在 N 维空间中的方向数,称为该张量的 Rank。
Rank 用 R 表示。
Scalar 是单个数字。
- 它有 0 个轴
- 它的 Rank 为 0
- 它是 0 维 Tensor
Vector 是一个数字数组。
- 它有 1 个轴
- 它的 Rank 为 1
- 它是 1 维 Tensor
Matrix 是一个 2 维数组。
- 它有 2 个轴
- 它的 Rank 为 2
- 它是 2 维 Tensor
真实 Tensor
严格来说,以上所有都是张量,但当我们谈论张量时,我们通常指的是维度大于 2 (R > 2) 的矩阵。
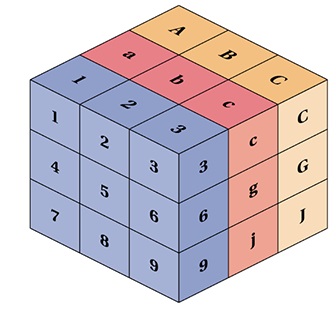
JavaScript 中的线性代数
在线性代数中,最简单的数学对象是 Scalar
const scalar = 1;
另一个简单的数学对象是 Array
const array = [ 1, 2, 3 ];
Matrices 是 2 维 Arrays
const matrix = [ [1,2],[3,4],[5,6] ];
Vectors 可以写成只有一列的 Matrices
const vector = [ [1],[2],[3] ];
Vectors 也可以写成 Arrays
const vector = [ 1, 2, 3 ];
Tensors 是 N 维 Arrays
const tensor = [ [1,2,3],[4,5,6],[7,8,9] ];
JavaScript 中的 Tensor 操作
在 JavaScript 中编程 Tensor 操作,很容易变成一团乱麻的循环。
使用 JavaScript 库可以为您省去很多麻烦。
用于 Tensor 操作的最常用库之一称为 tensorflow.js。
Tensor 加法
const tensorA = tf.tensor([[1, 2], [3, 4], [5, 6]]);
const tensorB = tf.tensor([[1,-1], [2,-2], [3,-3]]);
// Tensor 加法
const tensorAdd = tensorA.add(tensorB);
// 结果 [ [2, 1], [5, 2], [8, 3] ]
Tensor 减法
const tensorA = tf.tensor([[1, 2], [3, 4], [5, 6]]);
const tensorB = tf.tensor([[1,-1], [2,-2], [3,-3]]);
// Tensor 减法
const tensorSub = tensorA.sub(tensorB);
// 结果 [ [0, 3], [1, 6], [2, 9] ]

