分布
- 什么是正态分布?
- 什么是误差幅度?
- 什么是偏度?
- 什么是峰度?
正态分布
正态分布曲线呈钟形。
曲线的每个波段宽度为1个标准差
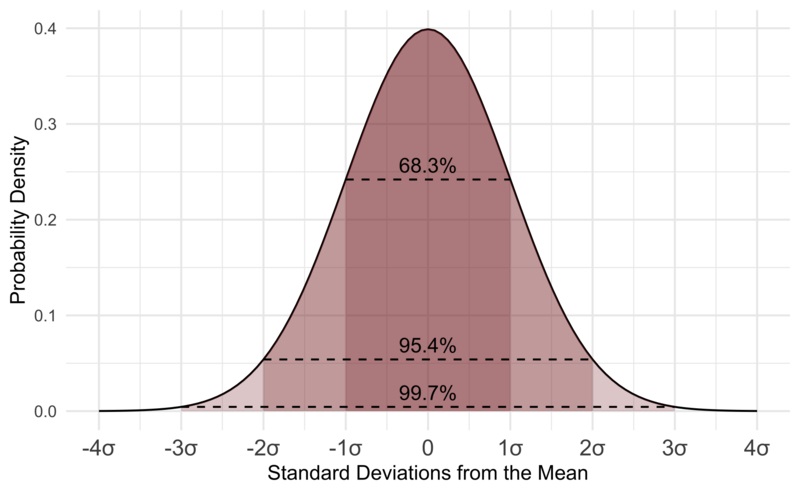
曲线的每个波段宽度为距平均值1个标准差。
距离1个标准差以内的值占68.27%。
距离2个标准差以内的值占95.45%。
距离3个标准差以内的值占99.73%。
这意味着什么?
大多数观测值都在距平均值1个标准差以内。
几乎所有观测值都在2个标准差以内。
实际上所有观测值都在3个标准差以内。
正态分布事实
正态分布是对称的。峰值总是将分布一分为二。
正态分布是概率分布。
许多观测值遵循正态分布
- 您的智商
- 您的体重
- 您的身高
- 您的薪水
- 您的血压
正态分布表明,接近平均值的值比远离平均值的值更频繁。
| 与平均值的距离 | 人口百分比 |
|---|---|
| 1个标准差 | 68.27% |
| 2个标准差 | 95.45% |
| 3个标准差 | 99.73% |
68-95-99.7 法则(又称经验法则)是一种记住正态分布中不同波段内值百分比的速记法。
正态分布也称为高斯分布和钟形曲线。
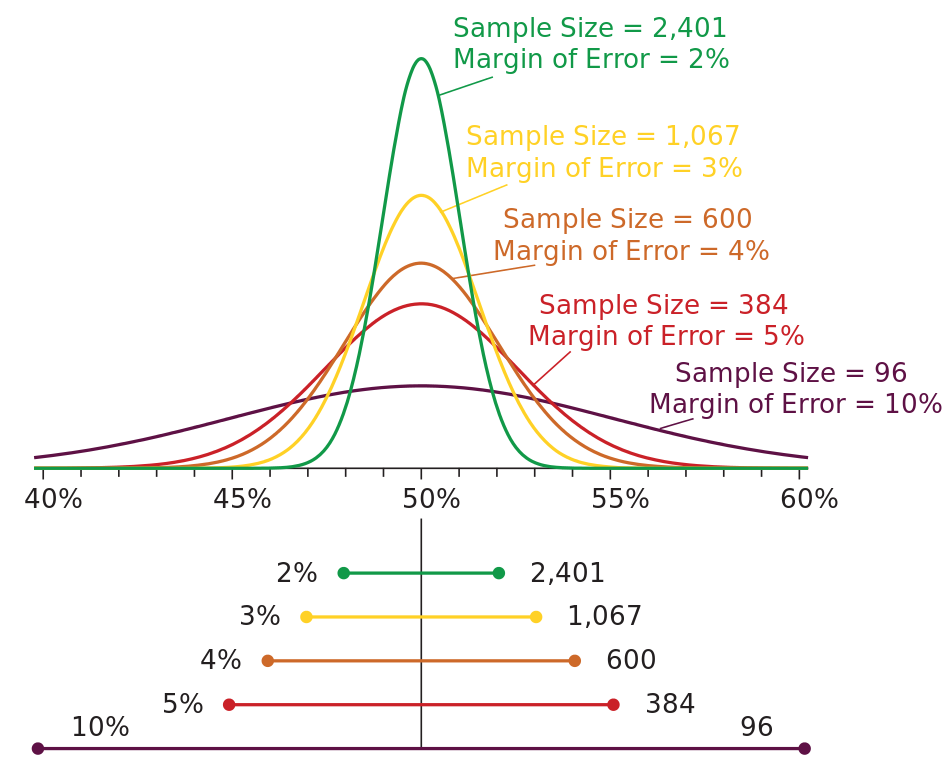
误差幅度
统计学家总是试图以100%的准确性预测一切。
但是,总会有一些不确定性。
误差幅度是量化这种统计不确定性的数字。
不同的幅度定义了我们认为可以找到正确答案的不同范围。
可接受的幅度是一个判断问题,并与答案的重要性有关。
我们收集的样本越多,误差幅度越低。
如何解释误差幅度
假设有55%的抽样人口表示他们计划投“赞成”票。
当将其推算到整个人口时,您需要加/减误差幅度,以给出可能的結果范围。
误差幅度为3%时,您可以确信有52%到58%的人会投“赞成”票。
误差幅度为10%时,您可以确信有45%到65%的人会投“赞成”票。
偏度(Skewness)
偏度是钟形曲线(正态分布)的一种扭曲(不对称)。
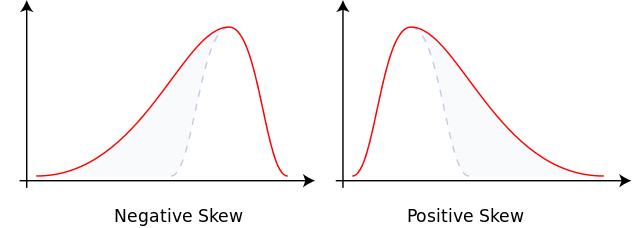
峰度(Kurtosis)
峰度也是正态分布(钟形曲线)的一种扭曲。
偏度描述了一个尾部的意外值,而峰度描述了两个尾部的意外值。
图:负峰度(低于正态分布)。
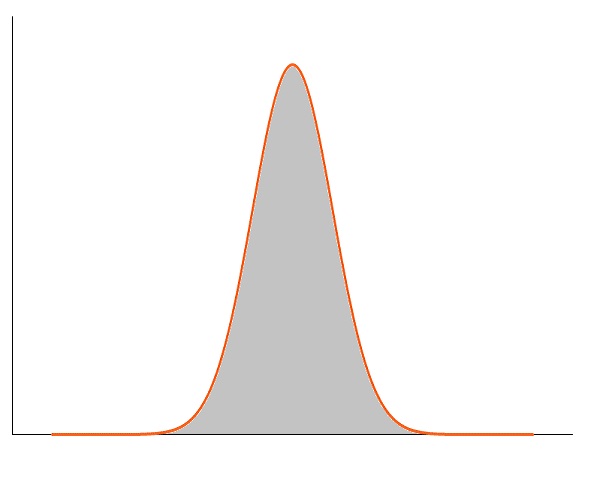
图:正峰度(高于正态分布)。