机器学习 - 训练/测试
评估您的模型
在机器学习中,我们创建模型来预测某些事件的结果,就像在前一章中,我们预测了已知汽车重量和发动机尺寸时的二氧化碳排放量。
为了衡量模型是否足够好,我们可以使用一种叫做“训练/测试”的方法。
什么是训练/测试?
训练/测试是一种衡量模型准确性的方法。
它之所以被称为训练/测试,是因为您将数据集分成两部分:训练集和测试集。
80% 用于训练,20% 用于测试。
您使用训练集来**训练**模型。
您使用测试集来**测试**模型。
**训练**模型意味着**创建**模型。
**测试**模型意味着测试模型的准确性。
从数据集开始
从您想要测试的数据集开始。
我们的数据集展示了商店中 100 名顾客及其购物习惯。
示例
import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
plt.scatter(x, y)
plt.show()
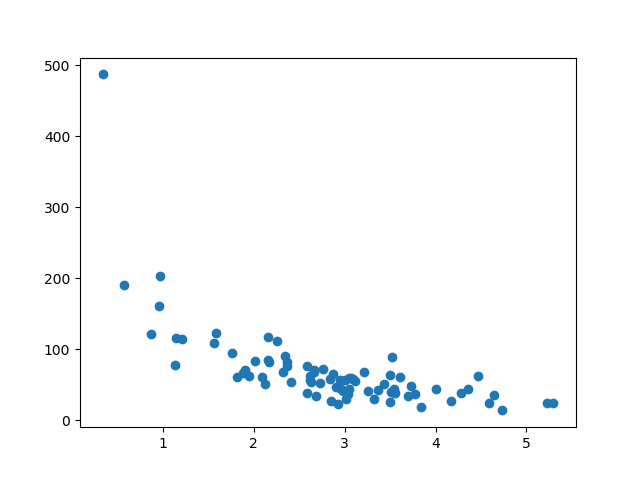
结果
x 轴表示购买前停留的分钟数。
y 轴表示购买时花费的金额。
分成训练/测试
**训练**集应该是原始数据中 80% 的随机选择。
**测试**集应该是剩余的 20%。
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
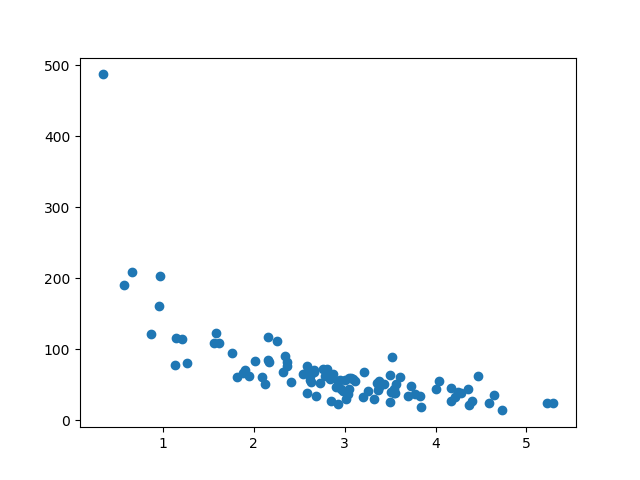
显示训练集
使用训练集显示相同的散点图
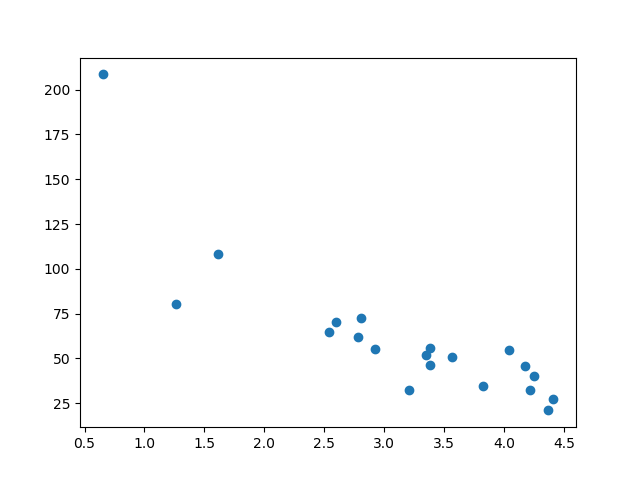
显示测试集
为了确保测试集没有完全不同,我们也会查看测试集。
拟合数据集
这个数据集看起来像什么?在我看来,我认为最适合的将是多项式回归,所以让我们画一条多项式回归线。
要绘制一条穿过数据点的线,我们使用 matplotlib 模块的 plot() 方法。
示例
绘制一条穿过数据点的多项式回归线
import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
myline = numpy.linspace(0, 6, 100)
plt.scatter(train_x, train_y)
plt.plot(myline, mymodel(myline))
plt.show()
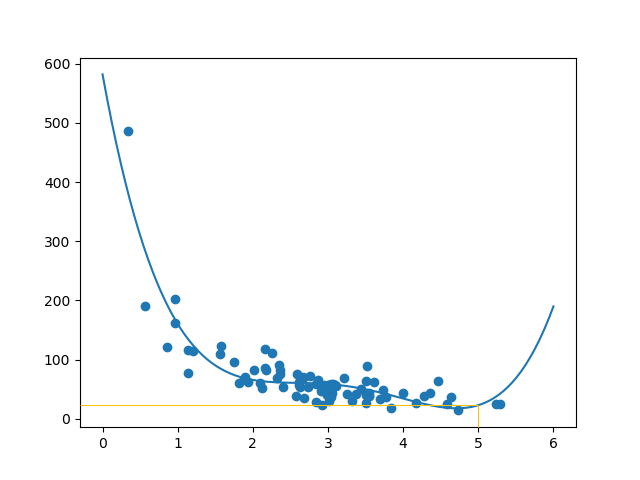
结果
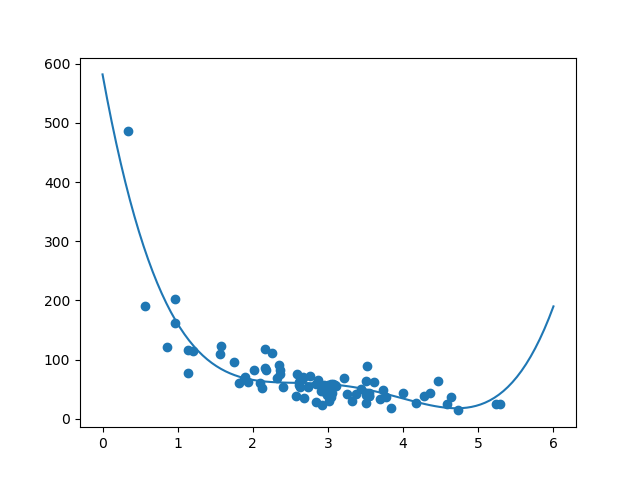
结果可以支持我对数据集适合多项式回归的建议,尽管如果我们尝试预测数据集之外的值,它会给出一些奇怪的结果。例如:该线表示在商店停留 6 分钟的顾客将进行价值 200 的购买。这可能是一种过拟合的迹象。
但是 R 方分数呢?R 方分数是衡量我的数据集拟合模型程度的一个很好的指标。
R2
还记得 R2,也称为 R 方吗?
它衡量 x 轴和 y 轴之间的关系,其值范围从 0 到 1,其中 0 表示没有关系,1 表示完全相关。
sklearn 模块有一个名为 r2_score() 的方法,可以帮助我们找到这种关系。
在这种情况下,我们希望衡量顾客在商店停留的分钟数与他们花费的金额之间的关系。
示例
我的训练数据在多项式回归中的拟合程度如何?
import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
r2 = r2_score(train_y, mymodel(train_x))
print(r2)
自己动手试一试 »
注意:结果 0.799 表明存在良好的关系。
引入测试集
现在我们已经建立了一个还不错的模型,至少在训练数据方面是这样。
现在我们还想用测试数据来测试模型,看看它是否给出相同的结果。
示例
让我们找出使用测试数据时的 R2 分数
import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
r2 = r2_score(test_y, mymodel(test_x))
print(r2)
自己动手试一试 »
注意:结果 0.809 表明模型也拟合测试集,我们有信心可以使用该模型来预测未来值。
预测值
既然我们已经确定我们的模型是好的,我们就可以开始预测新值了。
该示例预测顾客将花费 22.88 美元,这似乎与图表相符。