机器学习 - 混淆矩阵
在此页面上,W3schools.com 与 纽约数据科学学院 合作,为我们的学生提供数字培训内容。
什么是混淆矩阵?
它是一个在分类问题中用于评估模型错误所在的表格。
行代表实际应该为的类别。列代表我们做出的预测。使用此表格可以轻松查看哪些预测是错误的。
创建混淆矩阵
可以通过逻辑回归进行的预测来创建混淆矩阵。
现在,我们将使用 NumPy 来生成实际值和预测值。
import numpy
接下来,我们需要生成“实际”和“预测”值的数字。
actual = numpy.random.binomial(1, 0.9, size = 1000)
predicted = numpy.random.binomial(1, 0.9, size = 1000)
为了创建混淆矩阵,我们需要从 sklearn 模块导入 metrics。
from sklearn import metrics
导入 metrics 后,我们就可以在实际值和预测值上使用混淆矩阵函数。
confusion_matrix = metrics.confusion_matrix(actual, predicted)
为了创建更易于理解的可视化显示,我们需要将表格转换为混淆矩阵显示。
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])
可视化显示需要我们从 matplotlib 导入 pyplot。
import matplotlib.pyplot as plt
最后,我们可以使用 pyplot 的 plot() 和 show() 函数来显示图表。
cm_display.plot()
plt.show()
观看整个示例的实际演示
示例
import matplotlib.pyplot as plt
import numpy
from sklearn import metrics
actual = numpy.random.binomial(1,.9,size = 1000)
predicted = numpy.random.binomial(1,.9,size = 1000)
confusion_matrix = metrics.confusion_matrix(actual, predicted)
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])
cm_display.plot()
plt.show()
结果
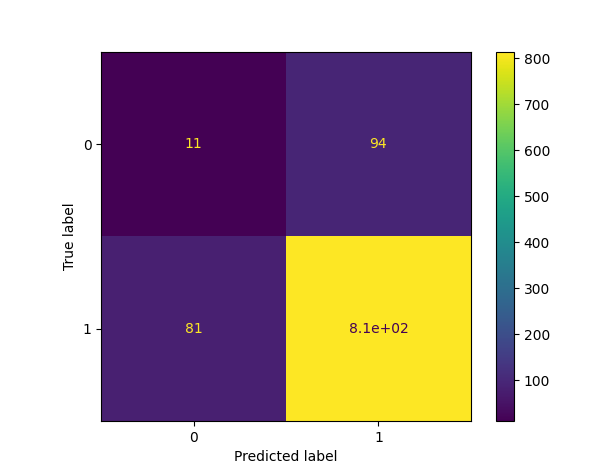
结果解释
创建的混淆矩阵有四个不同的象限
真负例(左上角象限)
假正例(右上角象限)
假负例(左下角象限)
真正例(右下角象限)
真表示预测值准确,假表示有错误或预测错误。
现在我们已经创建了一个混淆矩阵,我们可以计算不同的指标来量化模型的质量。首先,我们来看一下准确率。
广告
创建的指标
该矩阵为我们提供了许多有用的指标,可以帮助我们评估分类模型。
不同的度量包括:准确率、精确率、召回率(灵敏度)、特异度和 F1 分数,如下所述。
准确率
准确率衡量模型在多大程度上是正确的。
如何计算
(真正例 + 真负例) / 总预测数
精确率
在预测为正例的样本中,有多少比例是真正的正例?
如何计算
真正例 / (真正例 + 假正例)
精确率不评估正确预测的负例。
召回率(灵敏度)
在所有实际为正例的样本中,有多少比例被预测为正例?
召回率(有时也称为灵敏度)衡量模型预测正例的准确性。
这意味着它关注真正例和假负例(即被错误预测为负例的正例)。
如何计算
真正例 / (真正例 + 假负例)
召回率有助于理解模型预测某个实例为正例的程度。
特异度
模型预测负例的准确性如何?
特异度与召回率相似,但从负例的角度来看。
如何计算
真负例 / (真负例 + 假正例)
由于它与召回率正好相反,我们使用 recall_score 函数,传入相反的标签(pos_label=0)。
F1 分数
F1 分数是精确率和召回率的“调和平均数”。
它同时考虑了假正例和假负例,并且对于不平衡数据集很有用。
如何计算
2 * ((精确率 * 召回率) / (精确率 + 召回率))
此分数不考虑真负例。
所有计算合在一起
示例
#metrics
print({"Accuracy":Accuracy,"Precision":Precision,"Sensitivity_recall":Sensitivity_recall,"Specificity":Specificity,"F1_score":F1_score})
运行示例 »

