机器学习 - AUC - ROC 曲线
在此页面上,W3schools.com 与 纽约数据科学学院 合作,为我们的学生提供数字培训内容。
AUC - ROC 曲线
在分类中,有许多不同的评估指标。最流行的是准确率,它衡量模型正确的频率。这是一个很好的指标,因为它易于理解,并且通常希望获得最正确的猜测。在某些情况下,您可能需要考虑使用其他评估指标。
另一个常见的指标是 AUC,即接收者操作特征 (ROC) 曲线下的面积。接收者操作特征曲线绘制了不同分类阈值下的真阳性 (TP) 率与假阳性 (FP) 率。这些阈值是二元分类中分离两个类别的不同概率截止点。它使用概率来告诉我们模型分离类别的效果。
不平衡数据
假设我们有一个不平衡数据集,其中大部分数据都是一个值。我们可以通过预测多数类别来获得模型的高准确率。
示例
import numpy as np
来自 sklearn.metrics 导入 accuracy_score, confusion_matrix, roc_auc_score, roc_curve
n = 10000
ratio = .95
n_0 = int((1-ratio) * n)
n_1 = int(ratio * n)
y = np.array([0] * n_0 + [1] * n_1)
# 以下是从一个总是预测多数类别的假设模型中获得的概率
# 预测类别 1 的概率将是 100%
y_proba = np.array([1]*n)
y_pred = y_proba > .5
print(f'准确率分数: {accuracy_score(y, y_pred)}')
cf_mat = confusion_matrix(y, y_pred)
print('混淆矩阵')
print(cf_mat)
print(f'类别 0 准确率: {cf_mat[0][0]/n_0}')
print(f'类别 1 准确率: {cf_mat[1][1]/n_1}')
运行示例 »
广告
尽管我们获得了非常高的准确率,但该模型没有提供任何关于数据的信息,因此它没有用处。我们 100% 准确地预测类别 1,同时 0% 不准确地预测类别 0。以准确率为代价,拥有一个能够将两个类别在某种程度上分开的模型可能会更好。
示例
# 以下是从一个不总是预测众数的假设模型中获得的概率
y_proba_2 = np.array(
np.random.uniform(0, .7, n_0).tolist() +
np.random.uniform(.3, 1, n_1).tolist()
)
y_pred_2 = y_proba_2 > .5
print(f'准确率分数: {accuracy_score(y, y_pred_2)}')
cf_mat = confusion_matrix(y, y_pred_2)
print('混淆矩阵')
print(cf_mat)
print(f'类别 0 准确率: {cf_mat[0][0]/n_0}')
print(f'类别 1 准确率: {cf_mat[1][1]/n_1}')
运行示例 »
对于第二组预测,我们的准确率分数不如第一组高,但每个类别的准确率更平衡。使用准确率作为评估指标,我们会将第一个模型评价为高于第二个模型,尽管它没有告诉我们任何关于数据的信息。
在这种情况下,更倾向于使用 AUC 等其他评估指标。
import matplotlib.pyplot as plt
def plot_roc_curve(true_y, y_prob)
"""
绘制基于概率的 roc 曲线
"""
fpr, tpr, thresholds = roc_curve(true_y, y_prob)
plt.plot(fpr, tpr)
plt.xlabel('假阳性率')
plt.ylabel('真阳性率')
示例
模型 1
plot_roc_curve(y, y_proba)
print(f'模型 1 AUC 分数: {roc_auc_score(y, y_proba)}')
结果
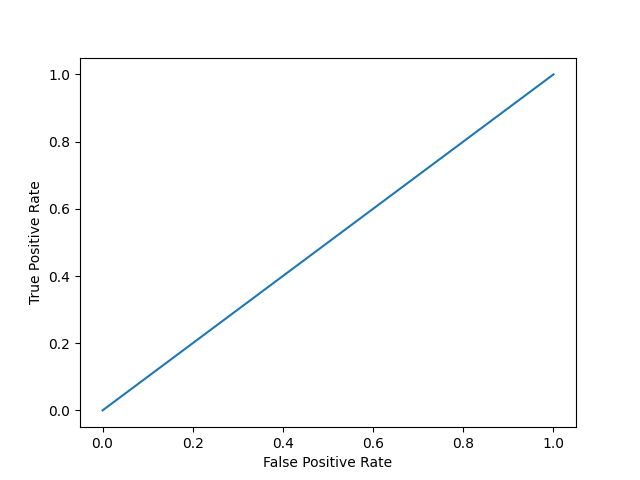
模型 1 AUC 分数: 0.5
示例
模型 2
plot_roc_curve(y, y_proba_2)
print(f'模型 2 AUC 分数: {roc_auc_score(y, y_proba_2)}')
结果
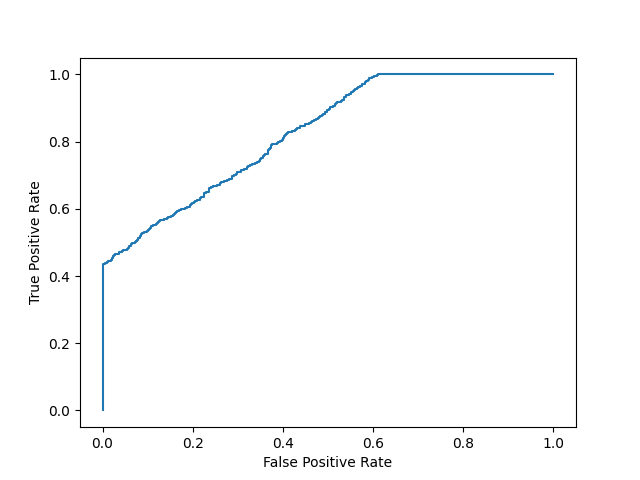
模型 2 AUC 分数: 0.8270551578947367
AUC 分数约为 0.5 表示模型无法区分两个类别,曲线看起来像一条斜率为 1 的直线。AUC 分数越接近 1,表示模型有能力区分两个类别,曲线将越接近图表的左上角。
概率
由于 AUC 是一个利用类别预测概率的指标,因此即使两个模型的准确率相似,我们也可以对 AUC 分数较高的模型比 AUC 分数较低的模型更有信心。
在下面的数据中,我们有两组来自假设模型的概率。第一组的概率在预测两个类别时不够“自信”(概率接近 0.5)。第二组的概率在预测两个类别时更“自信”(概率接近 0 或 1 的极端值)。
示例
import numpy as np
n = 10000
y = np.array([0] * n + [1] * n)
#
y_prob_1 = np.array(
np.random.uniform(.25, .5, n//2).tolist() +
np.random.uniform(.3, .7, n).tolist() +
np.random.uniform(.5, .75, n//2).tolist()
)
y_prob_2 = np.array(
np.random.uniform(0, .4, n//2).tolist() +
np.random.uniform(.3, .7, n).tolist() +
np.random.uniform(.6, 1, n//2).tolist()
)
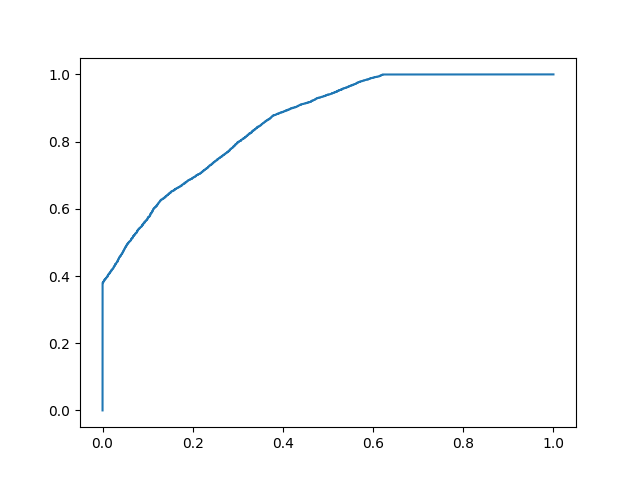
print(f'模型 1 准确率分数: {accuracy_score(y, y_prob_1>.5)}')
print(f'模型 2 准确率分数: {accuracy_score(y, y_prob_2>.5)}')
print(f'模型 1 AUC 分数: {roc_auc_score(y, y_prob_1)}')
print(f'模型 2 AUC 分数: {roc_auc_score(y, y_prob_2)}')
运行示例 »
尽管两个模型的准确率相似,但具有更高 AUC 分数的模型将更可靠,因为它考虑了预测概率。它在预测未来数据时更有可能为您提供更高的准确率。