数据科学 - 统计学 相关性 vs. 因果关系
相关性不代表因果关系
相关性衡量两个变量之间的数值关系。
高相关系数(接近 1)并不意味着我们可以确定两个变量之间存在实际关系。
一个经典的例子
- 夏天,海滩上的冰淇淋销量会增加
- 同时,溺水事故也会增加
这是否意味着冰淇淋销量增加是导致溺水事故增加的直接原因?
Python 中的海滩示例
这里,我们构建了一个虚构的数据集供您尝试
示例
import pandas as pd
import matplotlib.pyplot as plt
Drowning_Accident = [20,40,60,80,100,120,140,160,180,200]
Ice_Cream_Sale = [20,40,60,80,100,120,140,160,180,200]
Drowning = {"Drowning_Accident": [20,40,60,80,100,120,140,160,180,200],
"Ice_Cream_Sale": [20,40,60,80,100,120,140,160,180,200]}
Drowning = pd.DataFrame(data=Drowning)
Drowning.plot(x="Ice_Cream_Sale", y="Drowning_Accident", kind="scatter")
plt.show()
correlation_beach = Drowning.corr()
print(correlation_beach)
自己动手试一试 »
输出
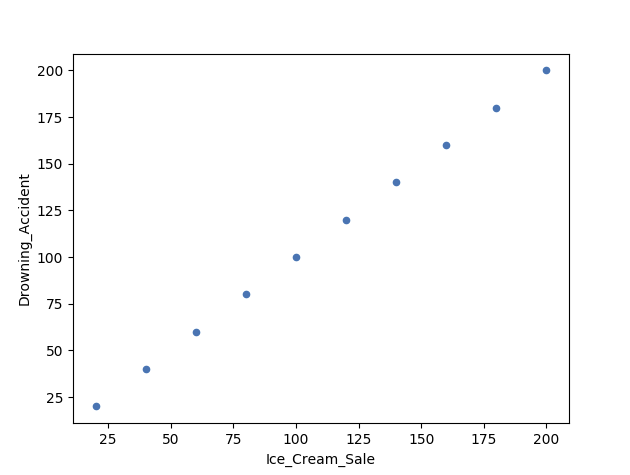
相关性 vs 因果关系 - 海滩示例
换句话说:我们能用冰淇淋销量来预测溺水事故吗?
答案是——可能不能。
这两个变量很可能是偶然相关的。
那么,是什么导致了溺水?
- 不熟练的游泳者
- 海浪
- 抽筋
- 癫痫
- 缺乏监督
- 酒精(不当)使用
- 等等。
让我们反过来论证
低相关系数(接近零)是否意味着 x 的变化不影响 y?
回到问题
- 我们能得出结论,由于相关系数较低,平均脉搏不会影响卡路里消耗吗?
答案是否定的。
相关性和因果关系之间存在重要区别
- 相关性是一个衡量数据有多密切相关的数字
- 因果关系是指 x 导致 y 的结论。
提示:在进行预测时,始终批判性地思考因果关系的概念!

