数据科学 - 数据准备
在分析数据之前,数据科学家必须提取数据,并使其干净且有价值。
使用 Pandas 提取和读取数据
在分析数据之前,必须先导入/提取数据。
在下面的示例中,我们将展示如何使用 Python 中的 Pandas 导入数据。
我们使用 read_csv() 函数导入带有健康数据的 CSV 文件
示例
import pandas as pd
health_data = pd.read_csv("data.csv", header=0, sep=",")
print(health_data)
自己动手试一试 »
示例解释
- 导入 Pandas 库
- 将数据框命名为
health_data。 header=0表示变量名的标题在第一行(请注意,在 Python 中 0 表示第一行)sep=","表示 "," 用作值之间的分隔符。这是因为我们使用的是 .csv 文件类型(逗号分隔值)
提示: 如果您的 CSV 文件很大,可以使用 head() 函数仅显示前 5 行
示例
import pandas as pd
health_data = pd.read_csv("data.csv", header=0, sep=",")
print(health_data.head())
自己动手试一试 »
数据清理
查看导入的数据。如您所见,数据是“脏”的,包含错误或未注册的值
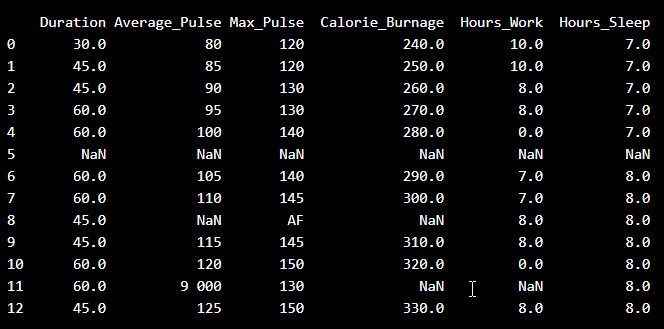
- 有些字段是空白的
- 平均脉搏 9000 是不可能的
- 由于空格分隔符,9000 将被视为非数字
- 最大脉搏的一个观测值被标记为“AF”,这没有意义
因此,我们必须清理数据才能进行分析。
删除空白行
我们看到非数字值(9000 和 AF)与缺失值在同一行。
解决方案:我们可以删除包含缺失观测值的行来解决这个问题。
当我们使用 Pandas 加载数据集时,所有空白单元格都会自动转换为“NaN”值。
因此,删除 NaN 单元格可以得到一个可以分析的干净数据集。
我们可以使用 dropna() 函数删除 NaN。axis=0 表示我们要删除所有包含 NaN 值的行
结果是没有 NaN 行的数据集
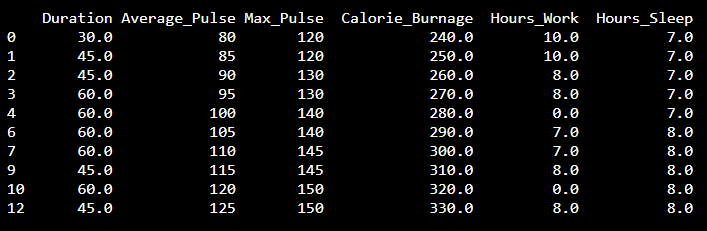
数据类别
为了分析数据,我们还需要了解我们正在处理的数据类型。
数据可以分为两类
- 定量数据 - 可以表示为数字或可以量化。可分为两类
- 离散数据:数字被计为“整数”,例如班级人数,足球比赛进球数
- 连续数据:数字可以是无限精度的。例如,一个人的体重,鞋码,温度
- 定性数据 - 不能表示为数字,也不能量化。可分为两类
- 标称数据:例如:性别、发色、种族
- 有序数据:例如:学校成绩(A、B、C),经济状况(低、中、高)
通过了解数据类型,您将能够知道分析数据时应使用哪种技术。
数据类型
我们可以使用 info() 函数列出我们数据中的数据类型:
结果
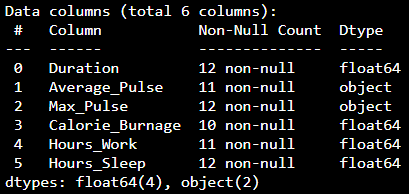
我们看到这个数据集有两种不同的数据类型
- Float64
- 对象
在这里,我们不能使用对象来进行计算和分析。我们必须将对象类型转换为 float64(在 Python 中,float64 是带小数的数字)。
我们可以使用 astype() 函数将数据转换为 float64。
以下示例将“Average_Pulse”和“Max_Pulse”转换为 float64 数据类型(其他变量已经是 float64 数据类型)
示例
health_data["Average_Pulse"] = health_data['Average_Pulse'].astype(float)
health_data["Max_Pulse"] = health_data["Max_Pulse"].astype(float)
print (health_data.info())
自己动手试一试 »
结果
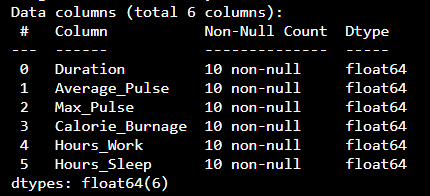
现在,数据集只有 float64 数据类型。
分析数据
清理完数据集后,我们就可以开始分析数据了。
我们可以在 Python 中使用 describe() 函数来总结数据
结果
| 持续时间 | Average_Pulse | Max_Pulse | Calorie_Burnage | Hours_Work | Hours_Sleep | |
|---|---|---|---|---|---|---|
| Count | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 |
| 均值 | 51.0 | 102.5 | 137.0 | 285.0 | 6.6 | 7.5 |
| Std | 10.49 | 15.4 | 11.35 | 30.28 | 3.63 | 0.53 |
| Min | 30.0 | 80.0 | 120.0 | 240.0 | 0.0 | 7.0 |
| 25% | 45.0 | 91.25 | 130.0 | 262.5 | 7.0 | 7.0 |
| 50% | 52.5 | 102.5 | 140.0 | 285.0 | 8.0 | 7.5 |
| 75% | 60.0 | 113.75 | 145.0 | 307.5 | 8.0 | 8.0 |
| Max | 60.0 | 125.0 | 150.0 | 330.0 | 10.0 | 8.0 |
- Count - 计算观测值的数量
- 均值 - 平均值
- Std - 标准差(在统计学章节中解释)
- Min - 最小值
- 25%, 50% 和 75% 是百分位数(在统计学章节中解释)
- Max - 最大值

