数据科学 - 统计学 相关性
相关性
相关性衡量两个变量之间的关系。
我们提到函数有一个预测值的目的,通过将输入(x)转换为输出(f(x))。我们也可以说函数使用两个变量之间的关系来进行预测。
相关系数
相关系数衡量两个变量之间的关系。
相关系数永远不会小于 -1 或大于 1。
- 1 = 变量之间存在完美的线性关系(例如,平均心率与卡路里消耗量)
- 0 = 变量之间不存在线性关系
- -1 = 变量之间存在完美的负线性关系(例如,工作时间越少,在训练期间卡路里消耗量越高)
完美的线性关系示例(相关系数 = 1)
我们将使用散点图来可视化平均心率和卡路里消耗量之间的关系(我们使用了运动手表的小数据集,共 10 个观测值)。
这次我们想要散点图,所以我们将 kind 改为“scatter”
示例
import matplotlib.pyplot as plt
health_data.plot(x ='Average_Pulse', y='Calorie_Burnage', kind='scatter')
plt.show()
自己动手试一试 »
输出
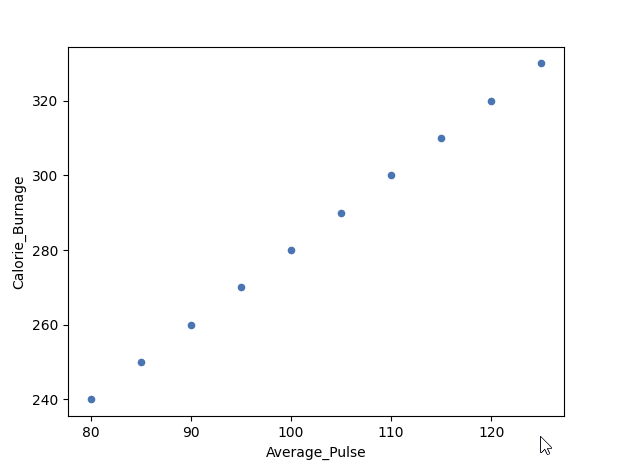
正如我们之前看到的,平均心率和卡路里消耗量之间存在完美的线性关系。
完美的负线性关系示例(相关系数 = -1)
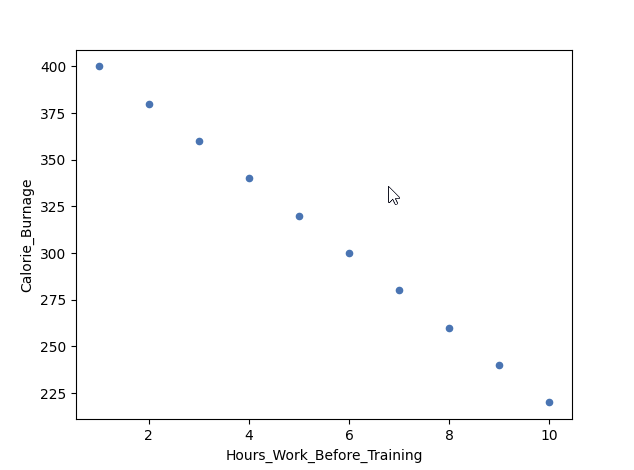
我们在此处绘制了虚构数据。x 轴表示训练前工作的小时数。y 轴是卡路里消耗量。
如果我们工作更长时间,我们可能会因为在训练前感到疲惫而消耗的卡路里更少。
此处的相关系数为 -1。
示例
import pandas as pd
import matplotlib.pyplot as plt
negative_corr = {'Hours_Work_Before_Training': [10,9,8,7,6,5,4,3,2,1],
'Calorie_Burnage': [220,240,260,280,300,320,340,360,380,400]}
negative_corr = pd.DataFrame(data=negative_corr)
negative_corr.plot(x ='Hours_Work_Before_Training', y='Calorie_Burnage', kind='scatter')
plt.show()
自己动手试一试 »
无线性关系示例(相关系数 = 0)
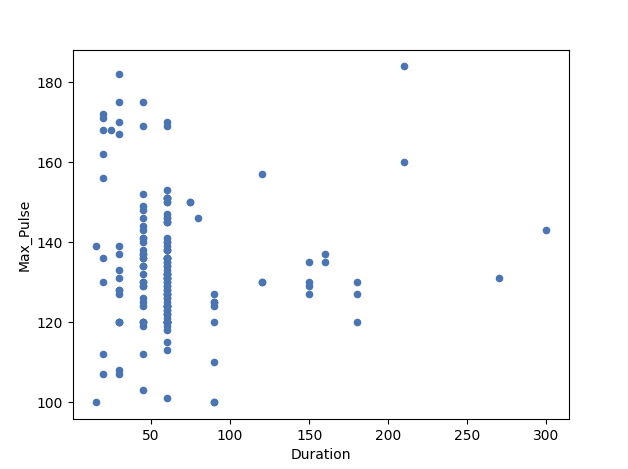
在这里,我们从 full_health_data 数据集中绘制了最大心率与时长。
正如你所见,这两个变量之间没有线性关系。这意味着更长的训练时间不会导致更高的最大心率。
此处的相关系数为 0。
示例
import matplotlib.pyplot as plt
full_health_data.plot(x ='Duration', y='Max_Pulse', kind='scatter')
plt.show()
自己动手试一试 »

